Giải đề thi học kì 2 toán lớp 10 năm 2019 - 2020 trường THPT Yên Mỹ - Hưng YênGiải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2019 - 2020 trường THPT Yên Mỹ - Hưng Yên với cách giải nhanh và chú ý quan trọng Quảng cáo
Đề bài Câu 1: Tam giác ABC có AB = c, BC = a, CA = b thỏa mãn \(b\left( {{b^2} - {a^2}} \right) = c\left( {{a^2} - {c^2}} \right)\). Số đo của góc A là A. \({90^0}\). B. \({60^0}\). C. \({45^0}\). D. \({30^0}\). Câu 2: Trong mặt phẳng Oxy, đường tròn \(\left( C \right)\) có tâm \(I\left( { - 2;\,\,1} \right)\) và tiếp xúc với đường thẳng \(\Delta :{\rm{3}}x-4y + 5 = 0\) có phương trình A. \({\left( {x + 2} \right)^2} + {\left( {y-1} \right)^2} = 4.\) B. \({\left( {x + 2} \right)^2} + {\left( {y-1} \right)^2} = \dfrac{1}{{25}}.\) C. \({\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 1.\) D. \({\left( {x + 2} \right)^2} + {\left( {y-1} \right)^2} = 1.\) Câu 3: Cho các mệnh đề sau I.\(\sin \dfrac{{11\pi }}{6} \ne \sin \left( {\dfrac{{5\pi }}{6} + 1505\pi } \right)\) II. \({\rm{ }}\sin k\pi = {\left( { - 1} \right)^k},k \in \mathbb{Z}\) III. \({\rm{ }}\cos k\pi = {\left( { - 1} \right)^k},k \in \mathbb{Z}\) . Mệnh đề nào đúng? A. Chỉ I và II. B. Chỉ I. C. Chỉ I và III. D. Chỉ III. Câu 4: Cho tam giác \(ABC\) có \(AB = 10\), \(AC = 12\), \(\widehat A = {150^0}\). Diện tích của tam giác \(ABC\) là A. \(60\sqrt 3 \). B. \(30\). C. \(60\). D. \(30\sqrt 3 \). Câu 5: Bảng xét dấu sau là của biểu thức nào? A. f(x)= –2x+10 B. f(x)= x2 – 25 C. f(x)= 2x –10 D. f(x)= –x2 + 25 Câu 6: Bất phương trình nào trong các bất phương trình sau có tập nghiệm \(S = \left( { - \infty ;1} \right) \cup \left( {4; + \infty } \right)\)? A. \( - {x^2} + 4x - 3 > 0\). B. \( - {x^2} + 5x - 4 > 0\). C. \({x^2} - 4x + 3 > 0\). D. \({x^2} - 5x + 4 > 0\). Câu 7: Từ một miếng tôn hình dạng là nửa đường tròn bán kính 1m người ta cắt ra một hình chữ nhật. Hỏi có thể cắt được miếng tôn có diện tích lớn nhất là bao nhiêu? A. 1 m2. B. 1.2 m2. C. 0,8 m2. D. 1,6m2. Câu 8: Cho đường thẳng (d):\(2x + 3y - 4 = 0\) . Vecto nào sau đây là vecto pháp tuyến của (d)? A. \(\overrightarrow {{n_3}} = \left( {2; - 3} \right)\). B. \(\overrightarrow {{n_2}} = \left( { - 4; - 6} \right)\). C. \(\overrightarrow {{n_1}} = \left( {3;2} \right)\). D. \(\overrightarrow {{n_4}} = \left( { - 2;3} \right)\). Câu 9: Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình\(\left\{ {\begin{array}{*{20}{c}}{2x + 3y - 1 > 0}\\{5x - y + 4 < 0}\end{array}} \right.\)? A. \(\left( {0;0} \right)\). B. \(\left( { - 2;0} \right)\). C. \(\left( { - 1; - 4} \right)\). D. \(\left( { - 3;4} \right)\) . Câu 10: Cho 3 đường thẳng có phương trình \({\Delta _1}:x + y + 3 = 0;\)\({\Delta _2}:x - y - 4 = 0;\)\({\Delta _3}:x - 2y = 0\) Tìm tọa độ điểm M nằm trên \({\Delta _3}\) sao cho khoảng cách từ M đến \({\Delta _1}\) bằng 2 lần khoảng cách từ M đến \({\Delta _2}\). A. \(M\left( {0;0} \right)\) B. \(M\left( { - 22; - 11} \right)\). C. \({M_1}\left( { - 22; - 11} \right),\,\,{M_2}\left( {2;1} \right)\). D. \(\,M\left( {2;1} \right)\). Câu 11: Tìm các giá trị của tham số m để phương trình \({x^2} - mx + 4m = 0\) vô nghiệm. A. \(0 \le m \le 16.\) B. \(0 < m < 16.\) C. \( - 4 < m < 4.\) D. \(0 < m < 4.\) Câu 12: Với \(x\) thuộc tập hợp nào dưới đây thì nhị thức bậc nhất\(f\left( x \right) = x + 3\) không âm? A. \(\left( { - \infty ; - 3} \right]\). B. \(\left[ { - 3; + \infty } \right)\). C. \(( - \infty ; - 3)\). D. \(\left( { - 3; + \infty } \right)\). Câu 13: Giá trị nhỏ nhất của hàm số \(f\left( x \right) = \dfrac{{{x^2} - x + 1}}{{x - 1}},x > 1\) là A. 2. B. 4. C. 5. D. 3. Câu 14: Tam giác ABC có AB = 5, BC = 8, CA = 6. Gọi G là trọng tâm tam giác, độ dài đoạn thẳng CG bằng bao nhiêu? A. \(\dfrac{{5\sqrt 7 }}{2}\). B. \(\dfrac{{13}}{3}\). C. \(\dfrac{{5\sqrt 7 }}{6}\). D. \(\dfrac{{5\sqrt 7 }}{3}\). Câu 15: Bất phương trình \(\dfrac{2}{{x + 1}} \ge x\) có tập nghiệm là A. \(S = \left( { - \infty ; - 2} \right) \cup \left( { - 1;1} \right)\). B. \(S = \left( { - \infty ;2} \right]\backslash \left\{ 1 \right\}\). C. \(S = \left( { - \infty ; - 2} \right] \cup \left( { - 1;1} \right]\). D. \(S = \left[ { - 2;1} \right]\). Câu 16: Góc có số đo \(\dfrac{\pi }{9}\)đổi sang độ là A. \({25^{\rm{o}}}\). B. \({20^{\rm{o}}}\). C. \({18^{\rm{o}}}\). D. \({15^{\rm{o}}}\). Câu 17: Biểu thức \(A = \sqrt 2 - \dfrac{1}{{\sin \left( {x + 2021\pi } \right)}}\)\(.\sqrt {\dfrac{1}{{1 + \cos x}} + \dfrac{1}{{1 - \cos x}}} \) với \(\pi < x < 2\pi \)có kết quả rút gọn bằng A. \( - \sqrt 3 {\cot ^2}x\). B. \( - {\cot ^2}x\). C. \( - \sqrt 2 {\cot ^2}x\). D. \(\sqrt 2 {\cot ^2}x\) . Câu 18: Tổng các nghiệm nguyên của hệ bất phương trình sau \(\left\{ \begin{array}{l}{x^2} - 4 \le 0\\{x^2} - 6x + 5 > 0\end{array} \right.\)bằng A. 2. B. 3. C. –3. D. 6. Câu 19: Một đường tròn có bán kính \(15\). Độ dài cung trên đường tròn đó có số đo \(\dfrac{\pi }{6}\)bằng A. \(\dfrac{{5\pi }}{3}\). B. \(\dfrac{{2\pi }}{5}\). C. \(\dfrac{{5\pi }}{2}\). D. \(\dfrac{\pi }{3}\). Câu 20: Tam giác ABC có A. \({a^2} = {b^2} + {c^2} - bc\cos A\). B. \({a^2} = {b^2} + {c^2} + bc\cos A\). C. \({a^2} = {b^2} + {c^2} - 2bc\cos A\). D. \({a^2} = {b^2} + {c^2} + 2bc\cos A\). Câu 21: Giá trị \(x = - 3\) thuộc tập nghiệm của bất phương trình nào trong các bất phương trình sau đây? A. \(\left( {x + 3} \right)\left( {x + 2} \right) > 0\). B. \({\left( {x + 3} \right)^2}\left( {x + 2} \right) \le 0\). C. \(\dfrac{1}{{1 + x}} + \dfrac{2}{{3 + 2x}} > 0\). D. \(x + \sqrt {1 - {x^2}} \ge 0\). Câu 22: Tìm tập nghiệm S của bất phương trình \({x^2} + 4 > 0\). A. \(S = \left( { - 4;0} \right)\). B. \(S = \left( { - 2; + \infty } \right)\). C. \(S = \left( { - \infty ;\, - 4} \right) \cup \left( {0; + \infty } \right)\). D. \(S = R\). Câu 23: Trong mặt phẳng Oxy, cho đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 16\). Tọa độ tâm \(I\) và bán kính \(R\) của đường tròn là A. \(I\left( {1; - 3} \right),{\rm{ }}R = 16.\) B. \(I\left( { - 1;3} \right),{\rm{ }}R = 4.\) C. \(I\left( {1; - 3} \right),{\rm{ }}R = 4.\) D. \(I\left( { - 1;3} \right),{\rm{ }}R = 16.\) Câu 24: Trong mặt phẳng Oxy, cho điểm M(4;1), đường thẳng d qua M cắt tia Ox, Oy lần lượt tại A(a;0) và B(0;b) sao cho tam giác AOB có diện tích nhỏ nhất. Giá trị của \(a - 4b\) bằng A. 0. B. \( - 14\). C. 8 . D. \( - 2\). Câu 25: Viết phương trình tham số của đường thẳng (d) đi qua điểm A(-1 ; 2) và vuông góc với đường thẳng r : \(2x - y + 4 = 0\). A. \(\left\{ \begin{array}{l}x = - 1 + t\\y = 2 + 2t\end{array} \right.\) B. \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 + t\end{array} \right.\). C. \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 - t\end{array} \right.\). D. \(\left\{ \begin{array}{l}x = - 1 - 2t\\y = 2 - t\end{array} \right.\). Câu 26: Cho điểm \(M\) trên đường tròn lượng giác gốc \(A\), gắn với hệ trục toạ độ \(Oxy\). Nếu thì hoành độ điểm M bằng A. \({\left( { - 1} \right)^k}\). B. \( - 1\). C. \(1\). D. \(0\). Câu 27: Tập các giá trị của tham số m để phương trình \({x^3} - \left( {m + 4} \right){x^2}\)\( + 5\left( {2m + 1} \right)x - 16m - 2 = 0\) có ba nghiệm phân biệt có dạng \(S = \left( { - \infty ;a} \right) \cup \left( {b; + \infty } \right)\backslash \left\{ {\dfrac{c}{d}} \right\},\)\(a,b,c,d \in \mathbb{Z}\) . Khi đó \(a + b + c - d\)bằng A. 29. B. 28. C. 20. D. 21. Câu 28: Mệnh đề nào sau đây sai? A. \(\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}{\rm{ }}\left( {\cos \alpha \ne 0} \right).\) B. \({\sin ^2}\left( {2018\alpha } \right) + {\cos ^2}\left( {2018\alpha } \right)\)\( = 2018.\) C. \( - 1 \le \sin \alpha \le 1;\)\( - 1 \le \cos \alpha \le 1.\) D. \(\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }}{\rm{ }}\left( {\sin \alpha \ne 0} \right).\) Câu 29: Trong đường tròn lượng giác cho hình vuông MNPQ nội tiếp vẽ theo chiều ngược với chiều quay của kim đồng hồ, biết sđ\(\left( {OA,OM} \right) = {45^0} + k{360^0},k \in \mathbb{Z}\) . Khi đó sđ \(\left( {OA,OP} \right)\) bằng A. \( - {45^0} + n{360^0},n \in \mathbb{Z}\). B. \({45^0} + n{360^0},n \in \mathbb{Z}\) C. \({135^0} + n{360^0},n \in \mathbb{Z}\). D. \( - {135^0} + n{360^0},n \in \mathbb{Z}\). Câu 30: Với mọi số thực \(\alpha \) để biểu thức có nghĩa, giá trị \(\tan \left( {\dfrac{{2019\pi }}{2} - \alpha } \right)\) bằng A. \( - \,\cot \alpha .\) B. \(\tan \alpha .\) C. \( - \,\tan \alpha .\) D. \(\cot \alpha .\) Câu 31: Cho tam thức bậc hai \(f(x) = - {x^2} + 5x - 6\). Tìm \(x\) để \(f(x) \ge 0\). A. \(x \in \left( { - \infty ;2} \right) \cup \left( {3; + \infty } \right)\). B. \(x \in \left( { - \infty ;2} \right] \cup \left[ {3; + \infty } \right)\). C. \(x \in \left[ {2;3} \right]\). D. \(x \in \left[ {1;6} \right]\). Câu 32: Cho \(0 < \alpha < \dfrac{\pi }{2}.\) Khẳng định nào sau đây đúng? A. \(\sin (\alpha - \pi ) \ge 0\) . B. \(\sin (\alpha - \pi ) \le 0\) . C. \(\sin (\alpha - \pi ) > 0\) . D. \(\sin (\alpha - \pi ) < 0\) . Câu 33: Tìm cosin của góc giữa 2 đường thẳng r1 : \(x + 2y - 7 = 0\) và r2 : \(x - 3y + 9 = 0\). A. \( - \dfrac{{\sqrt 2 }}{2}\). B. \(\dfrac{1}{2}\). C. \(\dfrac{1}{2}\). D. \(\dfrac{{\sqrt 2 }}{2}\). Câu 34: Một đồng hồ treo tường, kim giờ dài \(10,57cm\) và kim phút dài \(13,34cm\).Trong 30 phút mũi kim giờ vạch lên cung tròn có độ dài là A. \(2,77cm\). B. \(2,8cm\). C. \(2,76cm\). D. \(2,78cm.\). Câu 35: Tập nghiệm của bất phương trình \(\dfrac{{5x + 1}}{2} + \sqrt {3 - x} \ge \dfrac{x}{2} + \sqrt {3 - x} \) là A. \(\left[ { - \dfrac{1}{4};3} \right).\) B. \(\left[ {\dfrac{1}{4}; + \infty } \right).\) C. \(\left[ { - \dfrac{1}{4};3} \right].\) D. \(\left[ { - \dfrac{1}{4}; + \infty } \right).\) Câu 36: Rút gọn biểu thức \(A = \sin \left( {2019\pi + x} \right) - \cos \left( {\dfrac{{2021\pi }}{2} - x} \right)\)\( + \cot \left( {2019\pi - x} \right) + \tan \left( {\dfrac{{2019\pi }}{2} - x} \right)\) . Câu 37: Tìm m để bất phương trình \(m{x^2} + 2\left( {m - 1} \right)x + 1 \le 0\) có nghiệm? Câu 38: Cho \(\sin \alpha = \dfrac{1}{{\sqrt 3 }}\), với \(0 < \alpha < \dfrac{\pi }{2}\). Tính giá trị của \({\rm{cos(}}\alpha {\rm{ + }}\dfrac{\pi }{3})\) ? Câu 39: Trong mặt phẳng Oxy, cho \(A\left( {3; - 1} \right),{\rm{ }}B\left( {1; - 5} \right)\) a) Viết phương trình đường tròn tâm là trung điểm I của AB và bán kính R=3. b) Tìm điểm M thuộc đường thẳng d: \(x - y + 1 = 0\) sao cho khoảng cách từ M đến đường thẳng AB bằng \(\sqrt 5 \). Câu 40: Giải bất phương trình \(\dfrac{{x + 1}}{{2x + 1}} \le \dfrac{{x - 3}}{{2x - 3}}\) . Lời giải chi tiết HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện: Ban chuyên môn Loigiaihay.com PHẦN I: TRẮC NGHIỆM
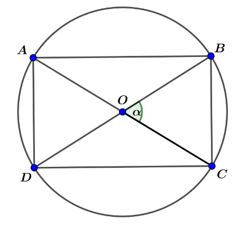
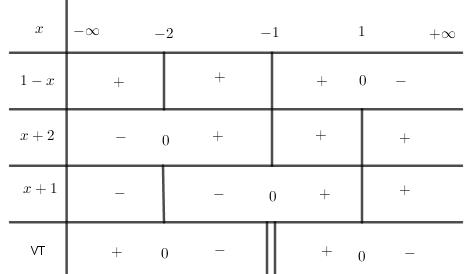
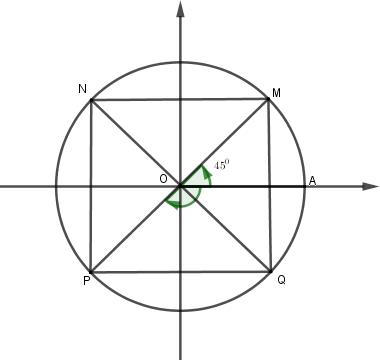
Câu 1 (VD): Phương pháp: Chuyển vế, phân tích thành nhân tử, từ đó suy ra mối quan hệ giữa a, b, c. Cách giải: Ta có: \(\begin{array}{l}b\left( {{b^2} - {a^2}} \right) = c\left( {{a^2} - {c^2}} \right)\\ \Leftrightarrow {b^3} - {a^2}b = c{a^2} - {c^3}\\ \Leftrightarrow {b^3} - {a^2}b - {a^2}c + {c^3} = 0\\ \Leftrightarrow \left( {{b^3} + {c^3}} \right) - \left( {{a^2}b + {a^2}c} \right) = 0\end{array}\) \( \Leftrightarrow \left( {b + c} \right)\left( {{b^2} - bc + {c^2}} \right)\)\( - {a^2}\left( {b + c} \right) = 0\) \( \Leftrightarrow \left( {b + c} \right)\left( {{b^2} - bc + {c^2} - {a^2}} \right) = 0\) \( \Leftrightarrow {b^2} - bc + {c^2} - {a^2} = 0\) (do \(b + c > 0\)) Áp dụng định lý Cosin trong tam giác ABC ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\) Thay vào đẳng thức cuối ta có: \(\begin{array}{l}{b^2} - bc + {c^2} - \left( {{b^2} + {c^2} - 2bc\cos A} \right) = 0\\ \Leftrightarrow - bc + 2bc\cos A = 0\\ \Leftrightarrow bc\left( {2\cos A - 1} \right) = 0\end{array}\) \( \Leftrightarrow 2\cos A - 1 = 0\) (do \(b > 0,c > 0\)) \( \Leftrightarrow \cos A = \dfrac{1}{2} \Rightarrow A = {60^0}\). Chọn B Câu 2 (TH): Phương pháp: Đường tròn (C) tâm I bán kính R tiếp xúc với đường thẳng \(\Delta \) \( \Leftrightarrow R = d\left( {I,\Delta } \right)\). Công thức viết phương trình đường tròn có tâm I(a; b) bán kính R là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) Cách giải: (C) tiếp xúc \(\Delta \) \( \Leftrightarrow R = d\left( {I,\Delta } \right)\) \( \Leftrightarrow R = \dfrac{{\left| {3.\left( { - 2} \right) - 4.1 + 5} \right|}}{{\sqrt {{3^2} + {{\left( { - 4} \right)}^2}} }} = 1\) Vậy \(\left( C \right)\) có phương trình: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 1\) Chọn D Câu 3 (TH): Phương pháp: Xét tính đúng sai của từng mệnh đề và kết luận. Cách giải: Mệnh đề I: \(\begin{array}{l}\sin \dfrac{{11\pi }}{6} = - \dfrac{1}{2}\\\sin \left( {\dfrac{{5\pi }}{6} + 1505\pi } \right) = - \dfrac{1}{2}\\ \Rightarrow \sin \dfrac{{11\pi }}{6} = \sin \left( {\dfrac{{5\pi }}{6} + 1505\pi } \right)\end{array}\) Do đó I đúng. Mệnh đề II: Cho \(k = 1\) thì \(\sin \pi = 0\) và \({\left( { - 1} \right)^1} = - 1\) nên \(\sin \pi \ne {\left( { - 1} \right)^1}\) Do đó II sai. Mệnh đề III: +) Nếu \(k = 2n,n \in \mathbb{Z}\) thì: \(\begin{array}{l}\cos k\pi = \cos \left( {2n\pi } \right) = 1\\{\left( { - 1} \right)^k} = {\left( { - 1} \right)^{2n}} = 1\end{array}\) \( \Rightarrow \cos k\pi = {\left( { - 1} \right)^k}\) khi \(k\) chẵn. +) Nếu \(k = 2n + 1,n \in \mathbb{Z}\) thì: \(\begin{array}{l}\cos k\pi = \cos \left( {2n + 1} \right)\pi \\ = \cos \left( {2n\pi + \pi } \right) = \cos \pi = - 1\\{\left( { - 1} \right)^k} = {\left( { - 1} \right)^{2n + 1}} = - 1\end{array}\) \( \Rightarrow \cos k\pi = {\left( { - 1} \right)^k}\) khi \(k\) lẻ. Vậy \(\cos k\pi = {\left( { - 1} \right)^k}\) với mọi \(k \in \mathbb{Z}\). Do đó III đúng. Chọn D Câu 4 (TH): Phương pháp: Sử dụng công thức tính diện tích \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin A\) Cách giải: Ta có: \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin A\) \( = \dfrac{1}{2}.10.12.\sin {120^0} = 30\sqrt 3 \) Chọn D Câu 5 (TH): Phương pháp: Quan sát dạng bảng xét dấu và đối chiếu đáp án. Cách giải: Ta thấy đây là bảng xét dấu của nhị thức bậc nhất. Loại B, D. Bên phải nghiệm cùng dấu với \(a\) nên \(a > 0\). Chọn C Câu 6 (TH): Phương pháp: Giải từng bpt và đối chiếu tập nghiệm. Cách giải: Đáp án A: \( - {x^2} + 4x - 3 > 0\) \( \Leftrightarrow 1 < x < 3\) Loại A. Đáp án B: \( - {x^2} + 5x - 4 > 0\) \( \Leftrightarrow 1 < x < 4\) Loại B. Đáp án C: \({x^2} - 4x + 3 > 0\) \( \Leftrightarrow \left[ \begin{array}{l}x > 3\\x < 1\end{array} \right.\) Loại C. Đáp án D: \({x^2} - 5x + 4 > 0\) \( \Leftrightarrow \left[ \begin{array}{l}x > 4\\x < 1\end{array} \right.\) Do đó tập nghiệm là \(S = \left( { - \infty ;1} \right) \cup \left( {4; + \infty } \right)\) Chọn D Câu 7 (VDC): Phương pháp: Tìm diện tích cắt được lớn nhất trên cả đường tròn. Từ đó suy ra diện tích lớn nhất trên nửa đường tròn. Cách giải: Xét đường tròn bán kính \(1\), ta cắt trên đó một hình chữ nhật \(ABCD\). Khi đó dễ thấy \({S_{AOB}} = {S_{BOC}} = {S_{COD}} = {S_{DOA}}\). \(\begin{array}{l}{S_{\Delta BOC}} = \dfrac{1}{2}OB.OC\sin \alpha \\ = \dfrac{1}{2}.1.1\sin \alpha = \dfrac{1}{2}\sin \alpha \\{S_{ABCD}} = 4{S_{\Delta BOC}} = 4.\dfrac{1}{2}\sin \alpha \\ = 2\sin \alpha \le 2.1 = 2\\ \Rightarrow {S_{ABCD}} \le 2\end{array}\) Do đó \({S_{ABCD}}\) đạt GTLN bằng \(2\) khi \(\sin \alpha = 1 \Leftrightarrow \alpha = {90^0}\). Vậy diện tích lớn nhất của miếng tôn cắt trên nửa đường tròn bằng \(1\). Chọn A Câu 8 (NB): Phương pháp: Đường thẳng \(ax + by + c = 0\) nhận \(\overrightarrow n = \left( {a;b} \right)\) làm 1 VTPT nên cũng nhận \(k\overrightarrow n = \left( {ka;kb} \right)\) làm một VTPT. Cách giải: Đường thẳng (d):\(2x + 3y - 4 = 0\) nhận \(\overrightarrow n = \left( {2;3} \right)\) làm 1 VTPT. Do đó (d) cũng nhận \(\overrightarrow {{n_2}} = - 2\overrightarrow n = \left( { - 4; - 6} \right)\) làm 1 VTPT. Chọn B Câu 9 (TH): Phương pháp: Thay tọa độ từng điểm vào mỗi hệ bất phương trình. Điểm nào có tọa độ thỏa mãn cả hai bpt trong hệ thì chọn. Cách giải: Đáp án A: sai do \(2.0 + 3.0 - 1 = - 1 < 0\) nên không thỏa mãn bpt đầu. Đáp án B: sai do \(2.\left( { - 2} \right) + 3.0 - 1 = - 5 < 0\) nên không thỏa mãn bpt đầu. Đáp án C: sai do \(2.\left( { - 1} \right) + 3.\left( { - 4} \right) - 1 = - 15 < 0\) nên không thỏa mãn bpt đầu. Đáp án D: đúng do \(\left\{ \begin{array}{l}2.\left( { - 3} \right) + 3.4 - 1 = 5 > 0\\5.\left( { - 3} \right) - 4 + 4 = - 15 < 0\end{array} \right.\) thỏa mãn cả hai bpt trong hệ. Chọn D Câu 10 (VD): Phương pháp: Tham số hóa tọa độ điểm M. Thay tọa độ M vào tính khoảng cách từ M đến \({\Delta _1}\) và \({\Delta _2}\). Lập phương trình và giải phương trình, từ đó suy ra tọa độ cần tìm. Cách giải: Ta có: \({\Delta _3}:x - 2y = 0 \Leftrightarrow x = 2y\). Cho \(x = t \in \mathbb{R}\) thì \(x = 2t\) ta được tọa độ điểm \(M \in {\Delta _3}\) là \(M\left( {2t;t} \right)\). \(d\left( {M,{\Delta _1}} \right) = \dfrac{{\left| {2t + t + 3} \right|}}{{\sqrt {{1^2} + {1^2}} }}\)\( = \dfrac{{\left| {3t + 3} \right|}}{{\sqrt 2 }}\) \(d\left( {M,{\Delta _2}} \right) = \dfrac{{\left| {2t - t - 4} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} }}\) \( = \dfrac{{\left| {t - 4} \right|}}{{\sqrt 2 }}\) \(\begin{array}{l}d\left( {M,{\Delta _1}} \right) = 2d\left( {M,{\Delta _2}} \right)\\ \Leftrightarrow \dfrac{{\left| {3t + 3} \right|}}{{\sqrt 2 }} = 2.\dfrac{{\left| {t - 4} \right|}}{{\sqrt 2 }}\\ \Leftrightarrow \left| {3t + 3} \right| = 2\left| {t - 4} \right|\\ \Leftrightarrow \left[ \begin{array}{l}3t + 3 = 2\left( {t - 4} \right)\\3t + 3 = - 2\left( {t - 4} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}3t + 3 = 2t - 8\\3t + 3 = - 2t + 8\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}t = - 11\\t = 1\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}M\left( { - 22; - 11} \right)\\M\left( {2;1} \right)\end{array} \right.\end{array}\) Vậy có hai điểm M thỏa mãn là \({M_1}\left( { - 22; - 11} \right),\,\,{M_2}\left( {2;1} \right)\) Chọn C Câu 11 (TH): Phương pháp: Phương trình bậc hai \(a{x^2} + bx + c = 0\left( {a \ne 0} \right)\) vô nghiệm \( \Leftrightarrow \Delta ' < 0\). Cách giải: Phương trình \({x^2} - mx + 4m = 0\) vô nghiệm \(\begin{array}{l} \Leftrightarrow \Delta < 0\\ \Leftrightarrow {m^2} - 4.4m < 0\\ \Leftrightarrow {m^2} - 16m < 0\\ \Leftrightarrow 0 < m < 16\end{array}\) Chọn B Câu 12 (TH): Phương pháp: Giải bpt \(f\left( x \right) \ge 0\) suy ra tập hợp cần tìm. Cách giải: Ta có: \(\begin{array}{l}f\left( x \right) \ge 0 \Leftrightarrow x + 3 \ge 0\\ \Leftrightarrow x \ge - 3\end{array}\) Vậy \(S = \left[ { - 3; + \infty } \right)\). Chọn B Câu 13 (TH): Phương pháp: Tách biểu thức thành \(x + \dfrac{1}{{x - 1}}\) rồi áp dụng bđt Cô si \(a + b \ge 2\sqrt {ab} \) với \(a,b > 0\) Cách giải: Ta có: \(\begin{array}{l}f\left( x \right) = \dfrac{{{x^2} - x + 1}}{{x - 1}} = \dfrac{{x\left( {x - 1} \right) + 1}}{{x - 1}}\\ = x + \dfrac{1}{{x - 1}} = x - 1 + \dfrac{1}{{x - 1}} + 1\end{array}\) Vì \(x > 1\) nên \(x - 1 > 0\). Áp dụng BĐT Cô si cho hai số \(x - 1\) và \(\dfrac{1}{{x - 1}}\) ta có: \(\begin{array}{l}x - 1 + \dfrac{1}{{x - 1}}\\ \ge 2\sqrt {\left( {x - 1} \right).\dfrac{1}{{x - 1}}} \\ = 2\sqrt 1 = 2\\ \Rightarrow f\left( x \right) = x - 1 + \dfrac{1}{{x - 1}} + 1\\ \ge 2 + 1 = 3\\ \Rightarrow f\left( x \right) \ge 3\end{array}\) Dấu “=” xảy ra khi \(x - 1 = \dfrac{1}{{x - 1}} \Leftrightarrow {\left( {x - 1} \right)^2} = 1\) \( \Leftrightarrow x = 2\) (do \(x > 1\)) Vậy GTNN của \(f\left( x \right)\) là \(3\). Chọn D Câu 14 (TH): Phương pháp: Tính độ dài trung tuyến \({m_c}\) theo công thức \(m_c^2 = \dfrac{{2\left( {{a^2} + {b^2}} \right) - {c^2}}}{4}\). Từ đó suy ra \(CG = \dfrac{2}{3}{m_c}\). Cách giải: Ta có: \(\begin{array}{l}m_c^2 = \dfrac{{2\left( {{a^2} + {b^2}} \right) - {c^2}}}{4}\\ = \dfrac{{2\left( {B{C^2} + C{A^2}} \right) - A{B^2}}}{4}\\ = \dfrac{{2\left( {{8^2} + {6^2}} \right) - {5^2}}}{4} = \dfrac{{175}}{4}\\ \Rightarrow {m_c} = \sqrt {\dfrac{{175}}{4}} = \dfrac{{5\sqrt 7 }}{2}\\ \Rightarrow CG = \dfrac{2}{3}{m_c} = \dfrac{2}{3}.\dfrac{{5\sqrt 7 }}{2} = \dfrac{{5\sqrt 7 }}{3}\end{array}\) Chọn D Câu 15 (VD): Phương pháp: Chuyển vế, quy đồng và xét dấu vế trái. Từ đó suy ra tập nghiệm. Cách giải: \(\begin{array}{l}\dfrac{2}{{x + 1}} \ge x \Leftrightarrow \dfrac{2}{{x + 1}} - x \ge 0\\ \Leftrightarrow \dfrac{{2 - {x^2} - x}}{{x + 1}} \ge 0\\ \Leftrightarrow \dfrac{{\left( {1 - x} \right)\left( {x + 2} \right)}}{{x + 1}} \ge 0\end{array}\) Ta có bảng xét dấu: Từ bảng xét dấu ta thấy \(VT \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \le - 2\\ - 1 < x \le 1\end{array} \right.\) Vậy tập nghiệm \(S = \left( { - \infty ; - 2} \right] \cup \left( { - 1;1} \right]\) Chọn C Câu 16 (TH): Phương pháp: Đổi đơn vị từ radian sang độ: \(\alpha \left( {rad} \right) = {\left( {\dfrac{{180\pi }}{\alpha }} \right)^0}\) Cách giải: Ta có: \(\dfrac{\pi }{9} = {\left( {\dfrac{{180.\dfrac{\pi }{9}}}{\pi }} \right)^0} = {20^0}\) Chọn B Câu 17 (VD): Phương pháp: Quy đồng, rút gọn biểu thức trong căn, chú ý dấu của \(\sin x\) khi \(\pi < x < 2\pi \). Sử dụng các công thức: \(\begin{array}{l}\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \\{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\\dfrac{1}{{{{\sin }^2}\alpha }} = 1 + {\cot ^2}\alpha \end{array}\) Cách giải: \(A = \sqrt 2 - \dfrac{1}{{\sin \left( {x + 2021\pi } \right)}}\)\(.\sqrt {\dfrac{1}{{1 + \cos x}} + \dfrac{1}{{1 - \cos x}}} \) \( = \sqrt 2 - \dfrac{1}{{\sin \left( {x + \pi + 2020\pi } \right)}}\) \(.\sqrt {\dfrac{{1 - \cos x + 1 + \cos x}}{{\left( {1 - \cos x} \right)\left( {1 + \cos x} \right)}}} \) \(\begin{array}{l} = \sqrt 2 - \dfrac{1}{{\sin \left( {x + \pi } \right)}}.\sqrt {\dfrac{2}{{1 - {{\cos }^2}x}}} \\ = \sqrt 2 - \dfrac{1}{{ - \sin x}}.\sqrt {\dfrac{2}{{{{\sin }^2}x}}} \\ = \sqrt 2 + \dfrac{1}{{\sin x}}.\dfrac{{\sqrt 2 }}{{\left| {\sin x} \right|}}\end{array}\) Do \(\pi < x < 2\pi \) nên \(\sin x < 0\) \( \Rightarrow \left| {\sin x} \right| = - \sin x\) \(\begin{array}{l} \Rightarrow A = \sqrt 2 + \dfrac{1}{{\sin x}}.\dfrac{{\sqrt 2 }}{{ - \sin x}}\\ = \sqrt 2 - \sqrt 2 .\dfrac{1}{{{{\sin }^2}x}}\\ = \sqrt 2 - \sqrt 2 .\left( {1 + {{\cot }^2}x} \right)\\ = \sqrt 2 - \sqrt 2 - \sqrt 2 {\cot ^2}x\\ = - \sqrt 2 {\cot ^2}x\end{array}\) Chọn C Câu 18 (VD): Phương pháp: Giải từng bất phương trình có trong hệ và suy ra tập nghiệm. Từ đó suy ra các giá trị nguyên của \(x\) thỏa mãn hệ phương trình và tính tổng. Cách giải: Ta có: \({x^2} - 4 \le 0 \Leftrightarrow - 2 \le x \le 2\) Do đó \({S_1} = \left[ { - 2;2} \right]\) \({x^2} - 6x + 5 > 0\) \( \Leftrightarrow \left[ \begin{array}{l}x > 5\\x < 1\end{array} \right.\) Do đó \({S_2} = \left( { - \infty ;1} \right) \cup \left( {5; + \infty } \right)\) Vậy \(S = {S_1} \cap {S_2} = \left[ { - 2;1} \right)\). Mà \(x\) nguyên nên \(x \in \left\{ { - 2; - 1;0} \right\}\). Tổng các nghiệm nguyên đó là: \( - 2 + \left( { - 1} \right) + 0 = - 3\) Chọn C Chú ý: Do đề bài hỏi tổng các nghiệm nguyên nên các em cộng các nghiệm lại, tránh chọn nhầm đáp án B là 3 nghiệm là sai. Câu 19 (VD): Phương pháp: Độ dài cung tròn có số đo \(\alpha \left( {rad} \right)\) là \(l = R\alpha \). Cách giải: Độ dài cung tròn có số đo \(\dfrac{\pi }{6}\) là: \(l = R\alpha = 15.\dfrac{\pi }{6} = \dfrac{{5\pi }}{2}\) Chọn C Câu 20 (NB): Phương pháp: Sử dụng định lí cô sin trong tam giác \({a^2} = {b^2} + {c^2} - 2bc\cos A\) Cách giải: Ta có: \({a^2} = {b^2} + {c^2} - 2bc\cos A\) Chọn C Câu 21 (TH): Phương pháp: Thay \(x = - 3\) vào từng bất phương trình và kiểm tra có thỏa mãn hay không. Cách giải: Với \(x = - 3\) thì: Đáp án A: \(0 > 0\) (sai) nên \(x = - 3\) không là nghiệm của bpt. Đáp án B: \(0 \le 0\) (đúng) nên \(x = - 3\) là nghiệm của bpt. Chọn B Câu 22 (TH): Phương pháp: Nhận xét vế trái của bpt, từ đó suy ra tập nghiệm. Cách giải: Ta thấy: \(\begin{array}{l}{x^2} \ge 0,\forall x \in \mathbb{R}\\ \Rightarrow {x^2} + 3 \ge 3,\forall x \in \mathbb{R}\\ \Rightarrow {x^2} + 3 > 0,\forall x \in \mathbb{R}\end{array}\) Vật bpt có tập nghiệm \(S = \mathbb{R}\) Chọn D Câu 23 (NB): Phương pháp: Đường tròn \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) có tâm \(I\left( {a;b} \right)\) bán kính \(R\). Cách giải: Đường tròn \(\left( C \right):{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} = 16\) có tâm \(I\left( {1; - 3} \right)\) bán kính \(R = 4\). Chọn C Câu 24 (VDC): Phương pháp: - Viết phương trình đường thẳng AB theo đoạn chắn. - Thay tọa độ điểm M và suy ra mối quan hệ giữa a và b. - Viết công thức tính diện tích tam giác AOB và đánh giá GTNN của diện tích. Cách giải: Đường thẳng AB đi qua \(A\left( {a;0} \right)\) và \(B\left( {0;b} \right)\) nên có phương trình \(\dfrac{x}{a} + \dfrac{y}{b} = 1\). \(M\left( {4;1} \right) \in AB \Leftrightarrow \dfrac{4}{a} + \dfrac{1}{b} = 1\) Do A, B thuộc các tia Ox, Oy nên \(a > 0,b > 0\). Tam giác AOB vuông tại O nên có diện tích là: \({S_{AOB}} = \dfrac{1}{2}OA.OB = \dfrac{1}{2}ab\) Áp dụng BĐT Cô si cho hai số dương \(\dfrac{4}{a}\) và \(\dfrac{1}{b}\) ta có: \(\dfrac{4}{a} + \dfrac{1}{b} \ge 2\sqrt {\dfrac{4}{a}.\dfrac{1}{b}} \) \( = 2.\dfrac{2}{{\sqrt {ab} }} = \dfrac{4}{{\sqrt {ab} }}\) \(\begin{array}{l} \Rightarrow 1 \ge \dfrac{4}{{\sqrt {ab} }} \Rightarrow \sqrt {ab} \ge 4\\ \Rightarrow ab \ge 16\end{array}\) \( \Rightarrow {S_{AOB}} = \dfrac{1}{2}ab \ge \dfrac{1}{2}.16 = 8\) Dấu “=” xảy ra khi \(\dfrac{4}{a} = \dfrac{1}{b} = \dfrac{1}{2} \Leftrightarrow \left\{ \begin{array}{l}a = 8\\b = 2\end{array} \right.\) Vậy \(a - 4b = 8 - 4.2 = 0\) Chọn A Câu 25 (TH): Phương pháp: Đường thẳng (d) vuông góc với \(\Delta \) thì nhận \(\overrightarrow {{n_\Delta }} \) làm VTCP. Cách giải: Ta có: \(\Delta :2x - y + 4 = 0\) \( \Rightarrow \overrightarrow {{n_\Delta }} = \left( {2; - 1} \right)\) là một VTPT của \(\Delta \). Đường thẳng (d) vuông góc với \(\Delta \) nên \(\overrightarrow {{u_d}} = \overrightarrow {{n_\Delta }} = \left( {2; - 1} \right)\) là VTCP. (d) đi qua \(A\left( { - 1;2} \right)\) nên có PTTS là: \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 - t\end{array} \right.,t \in \mathbb{R}\) Chọn C Câu 26 (NB): Phương pháp: Tìm tọa độ điểm M và suy ra kết luận. Cách giải: Nếu \(sd\left( {OA,OM} \right) = \dfrac{\pi }{2} + k2\pi \) thì \(M\left( {0;1} \right)\). Do đó hoành độ của M bằng \(0\). Chọn D Câu 27 (VDC): Phương pháp: Phân tích VT của phương trình thành nhân tử, từ đó tìm điều kiện của m để phương trình có 3 nghiệm phân biệt. Cách giải: Kiểm tra ta thấy \(x = 2\) là một nghiệm của phương trình. Do đó, \({x^3} - \left( {m + 4} \right){x^2}\) \( + 5\left( {2m + 1} \right)x - 16m - 2 = 0\) (1) \(\begin{array}{l} \Leftrightarrow \left( {x - 2} \right)\left[ {{x^2} - \left( {m + 2} \right)x + 8m + 1} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\{x^2} - \left( {m + 2} \right)x + 8m + 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 2\\{x^2} - \left( {m + 2} \right)x + 8m + 1 = 0\,\,\left( 2 \right)\end{array} \right.\end{array}\) Xét \(f\left( x \right) = {x^2} - \left( {m + 2} \right)x + 8m + 1\). Để (1) có 3 nghiệm phân biệt thì (2) phải có 2 nghiệm phân biệt khác \(2\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\Delta > 0\\f\left( 2 \right) \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 2} \right)^2} - 4\left( {8m + 1} \right) > 0\\{2^2} - \left( {m + 2} \right).2 + 8m + 1 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 4m + 4 - 32m - 4 > 0\\4 - 2m - 4 + 8m + 1 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 28m > 0\\6m + 1 \ne 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 28\\m < 0\end{array} \right.\\m \ne \dfrac{{ - 1}}{6}\end{array} \right.\end{array}\) Do đó \(m \in \left( { - \infty ;0} \right) \cup \left( {28; + \infty } \right)\backslash \left\{ {\dfrac{{ - 1}}{6}} \right\}\) \( \Rightarrow a = 0,b = 28,\) \(c = - 1,d = 6\) \( \Rightarrow a + b + c - d\) \( = 0 + 28 + \left( { - 1} \right) - 6 = 21\) Chọn D Câu 28 (TH): Phương pháp: Sử dụng đẳng thức lượng giác \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) Cách giải: Ta có: \({\sin ^2}\left( {2018\alpha } \right) + {\cos ^2}\left( {2018\alpha } \right) = 1\) nên B sai. Chọn B Câu 29 (VD): Phương pháp: Sử dụng tính chất hình vuông để tính \(\widehat {AOP}\) Từ đó suy ra số đo \(\left( {OA,OP} \right)\) với lưu ý chiều dương là ngược chiều quay của kim đồng hồ Cách giải: Vì \(MNPQ\) là hình vuông nên \(\widehat {POQ} = {90^0},\widehat {MOQ} = {90^0}\) Lại có \(\widehat {MOA} = {45^0}\) (gt) nên \(\widehat {AOQ} = {45^0}\) Suy ra \(\widehat {AOP} = {90^0} + {45^0} = {135^0}\) Do đó: sđ \(\left( {OA,OP} \right)\)\( = - {135^0} + k{360^0},k \in \mathbb{Z}\) Chọn D Chú ý: \(\widehat {AOP} = {135^0}\) nhưng góc \(\left( {OA,OP} \right)\) ngược chiều dương nên ta phải lấy giá trị âm là \( - {135^0}\), tránh nhầm lẫn chọn đáp án C là sai. Câu 30 (TH): Phương pháp: Sử dụng: \(\tan \left( {\alpha + k\pi } \right) = \tan \alpha \left( {k \in \mathbb{Z}} \right)\) \(\tan \left( {\dfrac{\pi }{2} - \alpha } \right) = \cot \alpha \) Cách giải: Ta có: \(\tan \left( {\dfrac{{2019\pi }}{2} - \alpha } \right)\)\( = \tan \left( {1009\pi + \dfrac{\pi }{2} - \alpha } \right)\) \( = \tan \left( {\dfrac{\pi }{2} - \alpha } \right) = \cot \alpha \) Chọn D Câu 31 (TH): Phương pháp: Đưa về giải bất phương trình \(A\left( x \right).B\left( x \right) \ge 0\) hoặc sử dụng dấu của tam thức bậc hai Cách giải: Ta có: \(f(x) \ge 0\) \(\begin{array}{l} \Leftrightarrow - {x^2} + 5x - 6 \ge 0\\ \Leftrightarrow {x^2} - 5x + 6 \le 0\\ \Leftrightarrow \left( {x - 2} \right)\left( {x - 3} \right) \le 0\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 2 \le 0\\x - 3 \ge 0\end{array} \right.\\\left\{ \begin{array}{l}x - 2 \ge 0\\x - 3 \le 0\end{array} \right.\end{array} \right.\\\end{array}\) \(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \le 2\\x \ge 3\end{array} \right.\\\left\{ \begin{array}{l}x \ge 2\\x \le 3\end{array} \right.\end{array} \right.\\ \Rightarrow 2 \le x \le 3\end{array}\) Vậy \(x \in \left[ {2;3} \right]\) Chọn C Câu 32 (TH): Phương pháp: Sử dụng dấu của các giá trị lượng giác của các cung thuộc góc phần tư thứ 2 Cách giải: Ta có: \(0 < \alpha < \dfrac{\pi }{2}\) \( \Leftrightarrow - \pi < \alpha - \pi < - \dfrac{\pi }{2}\)\( \Leftrightarrow \dfrac{\pi }{2} < \pi - \alpha < \pi \) Suy ra \(\sin \left( {\pi - \alpha } \right) > 0\) nên \(\sin \left( {\alpha - \pi } \right) < 0\) Chọn D Câu 33 (TH): Phương pháp: Sử dụng công thức góc giữa hai đường thẳng: Cho \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) Gọi góc giữa hai đường thẳng là \(\alpha \), ta có: \(\cos \alpha = \dfrac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} .\sqrt {a_2^2 + b_2^2} }}\) Cách giải: Gọi góc giữa hai đường thẳng trên là \(\alpha \), ta có \(\cos \alpha = \dfrac{{\left| {1.1 + 2.\left( { - 3} \right)} \right|}}{{\sqrt {{1^2} + {2^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }}\) \( = \dfrac{5}{{5\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}\) Chọn D Câu 34 (TH): Phương pháp: Sử dụng công thức tính độ dài cung tròn bán kính \(R\), số đo \(n\) là \(l = \dfrac{{\pi Rn}}{{180}}\) Cách giải: Trong \(30\) phút \( = \dfrac{1}{2}\) giờ thì kim giờ vạch lên cung tròn có số đo \(\dfrac{1}{2}.\dfrac{1}{{12}}{.360^0} = {15^0}\) Độ dài cung tròn đó là: \(l = \dfrac{{\pi .10,57.15}}{{180}} \approx 2,77cm\) Chọn A Câu 35 (VD): Phương pháp: Tìm điều kiện xác định, đưa về giải bất phương trình bậc nhất một ẩn. Cách giải: Điều kiện: \(3 - x \ge 0 \Leftrightarrow x \le 3\) Ta có: \(\dfrac{{5x + 1}}{2} + \sqrt {3 - x} \ge \dfrac{x}{2} + \sqrt {3 - x} \) \(\begin{array}{l} \Leftrightarrow \dfrac{{5x + 1}}{2} - \dfrac{x}{2} \ge 0\\ \Leftrightarrow 4x + 1 \ge 0\\ \Leftrightarrow x \ge - \dfrac{1}{4}\end{array}\) Vậy bất phương trình có tập nghiệm \(S = \left[ { - \dfrac{1}{4};3} \right].\) Chọn C PHẦN II: TỰ LUẬN Câu 36 (VD): Phương pháp: Sử dụng: \(\begin{array}{l}\sin \left( {\alpha + k2\pi } \right) = \sin \alpha \\\sin \left( {\alpha + \pi } \right) = - \sin \alpha \end{array}\) \(\begin{array}{l}\cot \left( {\alpha + k\pi } \right) = \cot \alpha \left( {k \in \mathbb{Z}} \right)\\\tan \left( {\alpha + k\pi } \right) = \tan \alpha \left( {k \in \mathbb{Z}} \right)\end{array}\) \(\cos \left( {\alpha + k2\pi } \right) = \cos \alpha \) \(\left( {k \in \mathbb{Z}} \right)\) \(\cos \left( {\dfrac{\pi }{2} - \alpha } \right) = \sin \alpha \) \(\tan \left( {\dfrac{\pi }{2} - \alpha } \right) = \cot \alpha \) Cách giải: Rút gọn biểu thức \(A = \sin \left( {2019\pi + x} \right) - \cos \left( {\dfrac{{2021\pi }}{2} - x} \right)\)\( + \cot \left( {2019\pi - x} \right) + \tan \left( {\dfrac{{2019\pi }}{2} - x} \right)\) Ta có: \(\begin{array}{l}\sin \left( {2019\pi + x} \right)\\ = \sin \left( {2018\pi + \pi + x} \right)\\ = \sin \left( {\pi + x} \right) = - \sin x\end{array}\) \(\cos \left( {\dfrac{{2021\pi }}{2} - x} \right) = \cos \left( {1010\pi + \dfrac{\pi }{2} - x} \right)\) \( = \cos \left( {\dfrac{\pi }{2} - x} \right) = \sin x\) \(\cot \left( {2019\pi - x} \right) = \cot \left( { - x} \right)\) \( = - \cot x\) \(\tan \left( {\dfrac{{2019\pi }}{2} - x} \right)\)\( = \tan \left( {1009\pi + \dfrac{\pi }{2} - x} \right)\) \( = \tan \left( {\dfrac{\pi }{2} - x} \right) = \cot x\) Do đó: \(A = - \sin x - \sin x - \cot x + \cot x\) \( = - 2\sin x\). Câu 37 (VD): Phương pháp: Sử dụng: Bất phương trình \(a{x^2} + bx + c \le 0\) có nghiệm với mọi \(x \in \mathbb{R}\) khi \(\left\{ \begin{array}{l}a < 0\\\Delta \le 0\end{array} \right.\) Lưu ý: Khi hệ số \(a\) chứa tham số \(m\) ta xét thêm trường hợp \(a = 0\). Khi \(\Delta > 0\) thì bất phương trình \(a{x^2} + bx + c \le 0\left( {a \ne 0} \right)\) luôn có nghiệm. Cách giải: Tìm m để bất phương trình \(m{x^2} + 2\left( {m - 1} \right)x + 1 \le 0\) có nghiệm? +) Với \(m = 0\) ta có bất phương trình \( - 2x + 1 \le 0 \Leftrightarrow x \ge \dfrac{1}{2}\) Bất phương trình có nghiệm nên nhận \(m = 0.\) +) Với \(m \ne 0\) Xét \(f\left( x \right) = m{x^2} + 2\left( {m - 1} \right)x + 1\) Ta có \(\Delta ' = {m^2} - 3m + 1\) Để \(f\left( x \right) \le 0\) có nghiệm thì \(\left[ \begin{array}{l}\Delta ' > 0\\\left\{ \begin{array}{l}m < 0\\\Delta ' \le 0\end{array} \right.\end{array} \right.\) \(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}{m^2} - 3m + 1 > 0\\\left\{ \begin{array}{l}m < 0\\{m^2} - 3m + 1 \le 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left[ \begin{array}{l}m > \dfrac{{3 + \sqrt 5 }}{2}\\m < \dfrac{{3 - \sqrt 5 }}{2}\end{array} \right.\\\left\{ \begin{array}{l}m < 0\\\dfrac{{3 - \sqrt 5 }}{2} \le m \le \dfrac{{3 + \sqrt 5 }}{2}\end{array} \right.\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}m \ge \dfrac{{3 + \sqrt 5 }}{2}\\m \le \dfrac{{3 - \sqrt 5 }}{2}\end{array} \right.\end{array}\) Vậy với \(\left[ \begin{array}{l}m \ge \dfrac{{3 + \sqrt 5 }}{2}\\m \le \dfrac{{3 - \sqrt 5 }}{2}\end{array} \right.\) thì bất phương trình đã cho có nghiệm. Câu 38 (VD): Phương pháp: Sử dụng: \(\cos \left( {a + b} \right)\)\( = \cos a\cos b - \sin a\sin b\) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) Cách giải: Cho\(\sin \alpha = \dfrac{1}{{\sqrt 3 }}\), với \(0 < \alpha < \dfrac{\pi }{2}\). Tính giá trị của \({\rm{cos(}}\alpha {\rm{ + }}\dfrac{\pi }{3})\) ? Ta có: \(\begin{array}{l}{\sin ^2}\alpha + {\cos ^2}\alpha = 1\\ \Leftrightarrow {\left( {\dfrac{1}{{\sqrt 3 }}} \right)^2} + {\cos ^2}\alpha = 1\\ \Leftrightarrow {\cos ^2}\alpha = \dfrac{2}{3}\end{array}\) \( \Rightarrow \cos \alpha = \dfrac{{\sqrt 6 }}{3}\) (do \(0 < \alpha < \dfrac{\pi }{2}\)) Lại có: \(\cos \left( {\alpha + \dfrac{\pi }{3}} \right)\) \( = \cos \alpha .\cos \dfrac{\pi }{3} - \sin \alpha .\sin \dfrac{\pi }{3}\) \(\begin{array}{l} = \dfrac{{\sqrt 6 }}{3}.\dfrac{1}{2} - \dfrac{1}{{\sqrt 3 }}.\dfrac{{\sqrt 3 }}{2}\\ = \dfrac{{\sqrt 6 }}{6} - \dfrac{1}{2}\\ = \dfrac{{\sqrt 6 - 3}}{6}\end{array}\) Câu 39 (VD): Phương pháp: a) Đường tròn tâm \(I\left( {{x_0};{y_0}} \right)\) và bán kính \(R\) có phương trình \({\left( {x - {x_0}} \right)^2} + {\left( {y - {y_0}} \right)^2} = {R^2}\) b) Khoảng cách từ \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(\Delta :ax + by + c = 0\) là: \(d\left( {M;\Delta } \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) Cách giải: Trong mặt phẳng Oxy, cho \(A\left( {3; - 1} \right),{\rm{ }}B\left( {1; - 5} \right)\) a) Viết phương trình đường tròn tâm là trung điểm I của AB và bán kính R=3. Trung điểm \(I\) của \(AB\) có tọa độ \(\left\{ \begin{array}{l}{x_I} = \dfrac{{{x_A} + {x_B}}}{2}\\{y_I} = \dfrac{{{y_A} + {y_B}}}{2}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_I} = \dfrac{{3 + 1}}{2} = 2\\{y_I} = \dfrac{{ - 1 + \left( { - 5} \right)}}{2} = - 3\end{array} \right.\) Vậy \(I\left( {2; - 3} \right)\) Phương trình đường tròn tâm \(I\left( {2; - 3} \right)\) và bán kính \(R = 3\) là \({\left( {x - 2} \right)^2} + {\left( {y + 3} \right)^2} = 9\) b) Tìm điểm M thuộc đường thẳng d: \(x - y + 1 = 0\) sao cho khoảng cách từ M đến đường thẳng AB bằng \(\sqrt 5 \). +) Ta có \(\overrightarrow {AB} = \left( { - 2; - 4} \right)\) là 1 VTCP của đường thẳng \(AB\) Suy ra \(\overrightarrow n = \left( {2; - 1} \right)\) là 1 VTPT của đường thẳng \(AB\) Phương trình đường thẳng \(AB\) đi qua \(A\left( {3; - 1} \right)\) và nhận \(\overrightarrow n = \left( {2; - 1} \right)\) là 1 VTPT là: \(2\left( {x - 3} \right) - 1\left( {y + 1} \right) = 0\) \( \Leftrightarrow 2x - y - 7 = 0\) Vì điểm \(M \in d:x - y + 1 = 0\) nên \(M\left( {{x_0};{x_0} + 1} \right)\) Theo đề bài ta có: \(\begin{array}{l}d\left( {M;\Delta } \right) = \sqrt 5 \\ \Leftrightarrow \dfrac{{\left| {2{x_0} - {x_0} - 1 - 7} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2}} }} = \sqrt 5 \\ \Leftrightarrow \dfrac{{\left| {{x_0} - 8} \right|}}{{\sqrt 5 }} = \sqrt 5 \\ \Leftrightarrow \left| {{x_0} - 8} \right| = 5\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} - 8 = 5\\{x_0} - 8 = - 5\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}{x_0} = 13 \Rightarrow {y_0} = 14\\{x_0} = 3 \Rightarrow {y_0} = 4\end{array} \right.\end{array}\) Vậy \(M\left( {13;14} \right)\) hoặc \(M\left( {3;4} \right)\) thỏa mãn điều kiện đề bài. Câu 40 (VD): Phương pháp: Chuyển vế rồi quy đồng, rút gọn các phân thức Đưa về giải bất phương trình \(\dfrac{{A\left( x \right)}}{{B\left( x \right)}} \le 0 \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}A\left( x \right) \ge 0\\B\left( x \right) < 0\end{array} \right.\\\left\{ \begin{array}{l}A\left( x \right) < 0\\B\left( x \right) > 0\end{array} \right.\end{array} \right.\) Cách giải: Giải bất phương trình \(\dfrac{{x + 1}}{{2x + 1}} \le \dfrac{{x - 3}}{{2x - 3}}\) Ta có: \(\dfrac{{x + 1}}{{2x + 1}} \le \dfrac{{x - 3}}{{2x - 3}}\) Điều kiện: \(x \ne - \dfrac{1}{2};x \ne \dfrac{3}{2}\) \(\begin{array}{l} \Leftrightarrow \dfrac{{x + 1}}{{2x + 1}} - \dfrac{{x - 3}}{{2x - 3}} \le 0\\ \Leftrightarrow \dfrac{{\left( {x + 1} \right)\left( {2x - 3} \right) - \left( {x - 3} \right)\left( {2x + 1} \right)}}{{\left( {2x + 1} \right)\left( {2x - 3} \right)}} \le 0\\ \Leftrightarrow \dfrac{{2{x^2} - x - 3 - \left( {2{x^2} - 5x - 3} \right)}}{{\left( {2x + 1} \right)\left( {2x - 3} \right)}} \le 0\\ \Leftrightarrow \dfrac{{4x}}{{\left( {2x + 1} \right)\left( {2x - 3} \right)}} \le 0\end{array}\) \(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 0\\\left( {2x + 1} \right)\left( {2x - 3} \right) < 0\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\\left( {2x + 1} \right)\left( {2x - 3} \right) > 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 0\\ - \dfrac{1}{2} < x < \dfrac{3}{2}\end{array} \right.\\\left\{ \begin{array}{l}x < 0\\\left[ \begin{array}{l}x < - \dfrac{1}{2}\\x > \dfrac{3}{2}\end{array} \right.\end{array} \right.\end{array} \right.\\ \Rightarrow \left[ \begin{array}{l}0 \le x < \dfrac{3}{2}\\x < - \dfrac{1}{2}\end{array} \right.\end{array}\) Vậy bất phương trình có tập nghiệm \(S = \left( { - \infty ; - \dfrac{1}{2}} \right) \cup \left[ {0;\dfrac{3}{2}} \right)\) Chú ý: Các em có thể lập bảng xét dấu của biểu thức \(\dfrac{{4x}}{{\left( {2x + 1} \right)\left( {2x - 3} \right)}}\) để suy ra tập nghiệm của bất phương trình. Loigiaihay.com
|





















Danh sách bình luận