Giải đề thi học kì 2 toán lớp 10 năm 2019 - 2020 trường THCS & THPT Nguyễn Tất ThànhGiải chi tiết đề thi học kì 2 môn toán lớp 10 năm 2019 - 2020 trường THCS & THPT Nguyễn Tất Thành với cách giải nhanh và chú ý quan trọng Quảng cáo
Đề bài Câu 1. Trong mặt phẳng tọa độ Oxy, cho hai điểm \(A(1;3)\)và \(B( - 3;5)\). Phương trình nào dưới đây là phương trình của đường tròn đường kính \(AB\)? A. \({(x - 1)^2} + {(y + 4)^2} = 5\) B. \({(x - 1)^2} + {(y + 4)^2} = 25\) C. \({(x + 1)^2} + {(y - 4)^2} = 25\) D. \({(x + 1)^2} + {(y - 4)^2} = 5\) Câu 2. Tìm tất cả các giá trị của tham số \(m\) để phương trình \({x^2} + {y^2} + 2mx - 4(m + 1)y\)\( + 4{m^2} + 5m + 2 = 0\) là phương trình của một đường tròn trong mặt phẳng tọa độ Oxy. A. \( - 2 < m < - 1\) B. \(\left[ \begin{array}{l}m < 1\\m > 2\end{array} \right.\) C. \(\left[ \begin{array}{l}m < - 2\\m > - 1\end{array} \right.\) D. \(\left[ \begin{array}{l}m \le - 2\\m \ge - 1\end{array} \right.\) Câu 3. Rút gọn biểu thức \(P = \frac{{2{{\cos }^2}x - 1}}{{\cos x + \sin x}}\) ta được A. \(P = |\cos x - \sin x|\) B. \(P = \sin x - \cos x\) C. \(P = \cos x - \sin x\) D. \(P = \cos x + \sin x\) Câu 4. Trong mặt phẳng tọa độ Oxy, cho đường tròn \((C):{\mkern 1mu} {\mkern 1mu} {(x + 1)^2} + {(y - 2)^2} = 9\) và đường thẳng \(\Delta :3x + 4y - 2m + 4 = 0\)(trong đó \(m\) là tham số). Gọi S là tập hợp tất cả các giá trị của tham số \(m\) sao cho đường thẳng \(\Delta \) là tiếp tuyến của đường tròn \((C)\). Tích các số thuộc tập hợp S bằng: A. \( - 36\) B. \(12\) C. \( - 56\) D. \( - 486\) Câu 5. Trong mặt phẳng tọa độ Oxy, cho đường tròn \((C):{\mkern 1mu} {\mkern 1mu} {x^2} + {y^2} - 2x + 4y + 1 = 0\). Tìm tọa độ tâm \(I\) và bán kính \(R\)của đường tròn \((C)\). A. \(I( - 1;2),R = 2\) B. \(I( - 1;2),R = 4\) C. \(I(1; - 2),R = 2\) D. \(I(1; - 2),R = 4\) Câu 6. Cho biết \(\frac{\pi }{2} < x < \pi \) và \(\sin x = \frac{1}{3}\). Tính \(\cos x\). A. \(\cos x = \frac{2}{3}\) B. \(\cos x = - \frac{2}{3}\) C. \(\cos x = \frac{{2\sqrt 2 }}{3}\) D. \(\cos x = - \frac{{2\sqrt 2 }}{3}\) Câu 7. Cho \(a,b \in \mathbb{R}\)là hai số thực bất kì. Xét các mệnh đề sau Mệnh đề 1: \(\sin (a + b)\)\( = \sin a\cos b + \sin b\cos a\). Mệnh đề 2: \(\sin (a - b)\)\( = \sin b\cos a - \sin a\cos b\). Mệnh đề 3: \(\cos (a - b)\)\( = \cos a\cos b - \sin a\sin b\). Mệnh đề 4: \(\cos (a + b)\)\( = \cos a\cos b + \sin a\sin b\). Số mệnh đề đúng trong các mệnh đề trên là: A. \(0\) B. \(1\) C. \(2\) D. \(3\) Câu 8. Cho biết \(\sin x + \cos x = - \frac{1}{2}\). Tính \(\sin 2x\). A. \(\sin 2x = - \frac{3}{4}\) B. \(\sin 2x = \frac{3}{4}\) C. \(\sin 2x = \frac{1}{2}\) D. \(\sin 2x = - 1\) Câu 9. Cho biết \(\tan x = 5\). Tính giá trị biểu thức \(Q = \frac{{3\sin x - 4\cos x}}{{\cos x + 2\sin x}}\). A. \(Q = 1\) B. \(Q = \frac{{19}}{{11}}\) C. \(Q = - 1\) D. \(Q = \frac{{11}}{9}\) Câu 10. Trong mặt phẳng tọa độ Oxy, cho elip \((E):{\mkern 1mu} {\mkern 1mu} \frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\). Tiêu cự của elip \((E)\) bằng A. \(4\) B. \(8\) C. \(16\) D. \(2\) Câu 11. Trong mặt phẳng tọa độ Oxy, cho hai điểm cố định là \(A(2;0)\), \(B(0;2)\). Cho biết quỹ tích các điểm \(M\)thỏa mãn điều kiện \(M{A^2} + M{B^2} = 12\) là một đường tròn bán kính \(R\). Tìm \(R\). A. \(R = \sqrt 5 \) B. \(R = 4\) C. \(R = \sqrt 3 \) D. \(R = 2\) Câu 12. Cho biết \(\sin x + \sin y = \sqrt 3 \) và \(\cos x - \cos y = 1\). Tính \(\cos (x + y)\). A. \(\cos (x + y) = 1\) B. \(\cos (x + y) = - 1\) C. \(\cos (x + y) = 0\) D. \(\cos (x + y) = \frac{1}{2}\) PHẦN II: TỰ LUẬN (7 điểm). Câu 1: (2 điểm) 1. Giải phương trình \(\sqrt {{x^2} - 2x + 6} = 2x - 1\). 2. Giải bất phương trình \(\sqrt { - {x^2} + 3x + 4} \le x + 1\). Câu 2: (2 điểm) 1. Cho biết \(\frac{\pi }{2} < a < \pi \) và \(\tan a = - 2\). Tính \(\cos a\) và \(\cos 2a\). 2. Cho tam giác \(ABC\). Chứng minh rằng \(\sin 2A + \sin 2B + \sin 2C \)\(= 4\sin A\sin B\sin C\). Câu 3: (2,5 điểm) 1. Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): \({x^2} + {y^2} - 6x + 4y - 12 = 0\). a) Viết phương trình tiếp tuyến của đường tròn (C) tại điểm \(A( - 1;1)\). b) Viết phương trình đường thẳng \(\Delta \) song song với đường thẳng \(d:3x - 4y - 2 = 0\) và cắt đường tròn (C) tại hai điểm \(A,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} B\) sao cho độ dài đoạn thẳng\(AB = 8\). 2. Trong mặt phẳng tọa độ Oxy, cho elip \((E):\;\;\frac{{{x^2}}}{4} + {y^2} = 1\). Gọi \({F_1},{F_2}\) là hai tiêu điểm của \((E)\) và điểm \(M \in (E)\) sao cho \(M{F_1} \bot M{F_2}\). Tính \(MF_1^2 + MF_2^2\) và diện tích \(\Delta M{F_1}{F_2}\). Câu 4: (0,5 điểm) Cho tam giác \(ABC\) có số đo ba góc là \(A,B,C\) thỏa mãn điều kiện \(\tan \frac{A}{2} + \tan \frac{B}{2} + \tan \frac{C}{2} = \sqrt 3 \). Chứng minh rằng tam giác \(ABC\) là tam giác đều. Lời giải chi tiết HƯỚNG DẪN GIẢI CHI TIẾT Thực hiện: Ban chuyên môn Loigiaihay.com PHẦN I: TRẮC NGHIỆM
Câu 1 (TH): Phương pháp: Đường tròn đường kính AB có tâm là trung điểm AB và bán kính \(R = \frac{{AB}}{2}\). Công thức viết phương trình đường tròn biết tâm \(I\left( {a;b} \right)\) bán kính \(R\) là: \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\) Cách giải: Gọi I là trung điểm của AB. Khi đó \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_A} + {x_B}}}{2}\\{y_I} = \frac{{{y_A} + {y_B}}}{2}\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}{x_I} = \frac{{1 + \left( { - 3} \right)}}{2} = - 1\\{y_I} = \frac{{3 + 5}}{2} = 4\end{array} \right.\) \( \Rightarrow I\left( { - 1;4} \right)\) \(AB = \sqrt {{{\left( { - 3 - 1} \right)}^2} + {{\left( {5 - 3} \right)}^2}} \) \( = 2\sqrt 5 \) Đường tròn đường kính AB có tâm \(I\left( { - 1;4} \right)\) bán kính \(R = \frac{{AB}}{2} = \frac{{2\sqrt 5 }}{2} = \sqrt 5 \) nên có phương trình: \({\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = {\left( {\sqrt 5 } \right)^2}\) hay \({\left( {x + 1} \right)^2} + {\left( {y - 4} \right)^2} = 5\) Chọn D Câu 2 (TH): Phương pháp: Phương trình \({x^2} + {y^2} - 2ax - 2by + c = 0\) là phương trình đường tròn \( \Leftrightarrow {a^2} + {b^2} - c > 0\). Cách giải: \({x^2} + {y^2} + 2mx - 4(m + 1)y\)\( + 4{m^2} + 5m + 2 = 0\) (1) Có \(a = - m,b = 2\left( {m + 1} \right),\) \(c = 4{m^2} + 5m + 2\) (1) là phương trình đường tròn \(\begin{array}{l} \Leftrightarrow {a^2} + {b^2} - c > 0\\ \Leftrightarrow {\left( { - m} \right)^2} + 4{\left( {m + 1} \right)^2}\\ - \left( {4{m^2} + 5m + 2} \right) > 0\\ \Leftrightarrow {m^2} + 4\left( {{m^2} + 2m + 1} \right)\\ - 4{m^2} - 5m - 2 > 0\\ \Leftrightarrow {m^2} + 4{m^2} + 8m + 4\\ - 4{m^2} - 5m - 2 > 0\\ \Leftrightarrow {m^2} + 3m + 2 > 0\\ \Leftrightarrow \left[ \begin{array}{l}m > - 1\\m < - 2\end{array} \right.\end{array}\) Chọn C Câu 3 (VD): Phương pháp: Sử dụng công thức: \(\begin{array}{l}\cos 2x = 2{\cos ^2}x - 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\cos ^2}x - {\sin ^2}x\end{array}\) Thay vào biểu thức và rút gọn. Cách giải: Ta có: \(\begin{array}{l}P = \frac{{2{{\cos }^2}x - 1}}{{\cos x + \sin x}} = \frac{{\cos 2x}}{{\cos x + \sin x}}\\ = \frac{{{{\cos }^2}x - {{\sin }^2}x}}{{\cos x + \sin x}}\\ = \frac{{\left( {\cos x - \sin x} \right)\left( {\cos x + \sin x} \right)}}{{\cos x + \sin x}}\\ = \cos x - \sin x\end{array}\) Chọn C Câu 4 (TH): Phương pháp: Đường thẳng \(\Delta \) là tiếp tuyến của đường tròn (C) tâm I bán kính R \( \Leftrightarrow d\left( {I,\Delta } \right) = R\) Cách giải: Đường tròn \((C):{(x + 1)^2} + {(y - 2)^2} = 9\) có tâm \(I\left( { - 1;2} \right)\) bán kính \(R = 3\). Đường thẳng \(\Delta \) là tiếp tuyến của đường tròn (C) \(\begin{array}{l} \Leftrightarrow d\left( {I,\Delta } \right) = R\\ \Leftrightarrow \frac{{\left| {3.\left( { - 1} \right) + 4.2 - 2m + 4} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 3\\ \Leftrightarrow \frac{{\left| {9 - 2m} \right|}}{5} = 3\\ \Leftrightarrow \left| {9 - 2m} \right| = 15\\ \Leftrightarrow \left[ \begin{array}{l}9 - 2m = 15\\9 - 2m = - 15\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}2m = - 6\\2m = 24\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 3\\m = 12\end{array} \right.\end{array}\) Do đó \(S = \left\{ { - 3;12} \right\}\) nên tích cần tìm bằng \(\left( { - 3} \right).12 = - 36\). Chọn A Câu 5 (NB): Phương pháp: Đường tròn \({x^2} + {y^2} - 2ax - 2by + c = 0\) có tâm \(I\left( {a;b} \right)\) bán kính \(R = \sqrt {{a^2} + {b^2} - c} \) Cách giải: \((C):{x^2} + {y^2} - 2x + 4y + 1 = 0\) Có \(a = 1,b = - 2,c = 1\) nên đường tròn (C) có tâm \(I\left( {1; - 2} \right)\) và bán kính \(R = \sqrt {{1^2} + {{\left( { - 2} \right)}^2} - 1} = 2\) Chọn C Câu 6 (TH): Phương pháp: Sử dụng công thức \({\sin ^2}x + {\cos ^2}x = 1\) để tính \({\cos ^2}x\) Kết hợp điều kiện của \(x\) để suy ra dấu của \(\cos x\) và kết luận. Cách giải: Ta có: \(\begin{array}{l}{\sin ^2}x + {\cos ^2}x = 1\\ \Rightarrow {\left( {\frac{1}{3}} \right)^2} + {\cos ^2}x = 1\\ \Rightarrow {\cos ^2}x = 1 - \frac{1}{9} = \frac{8}{9}\end{array}\) Mà \(\frac{\pi }{2} < x < \pi \) nên \(x\) thuộc góc phần tư thứ II \( \Rightarrow \cos x < 0\) Vậy \(\cos x = - \sqrt {\frac{8}{9}} = - \frac{{2\sqrt 2 }}{3}\) Chọn D Câu 7 (NB): Phương pháp: Sử dụng các công thức cộng để nhận xét từng mệnh đề. Cách giải: Ta có: \(\sin (a + b)\) \( = \sin a\cos b + \sin b\cos a\) nên mệnh đề 1 đúng. \(\sin (a - b)\) \( = \sin a\cos b - \sin b\cos a\)\( \ne \sin b\cos a - \sin a\cos b\) nên mệnh đề 2 sai. \(\cos (a - b)\) \( = \cos a\cos b + \sin a\sin b\) \( \ne \cos a\cos b - \sin a\sin b\) nên mệnh đề 3 sai \(\cos (a + b)\) \( = \cos a\cos b - \sin a\sin b\) \( \ne \cos a\cos b + \sin a\sin b\) nên mệnh đề 4 sai. Vậy có tất cả 1 mệnh đề đúng. Chọn B Câu 8 (VD): Phương pháp: Bình phương đẳng thức đã cho, sử dụng các công thức: \(\begin{array}{l}{\sin ^2}x + {\cos ^2}x = 1\\\sin 2x = 2\sin x\cos x\end{array}\) Cách giải: Ta có: \(\begin{array}{l}\sin x + \cos x = - \frac{1}{2}\\ \Rightarrow {\left( {\sin x + \cos x} \right)^2} = \frac{1}{4}\\ \Leftrightarrow {\sin ^2}x + {\cos ^2}x + 2\sin x\cos x = \frac{1}{4}\\ \Leftrightarrow 1 + 2\sin x\cos x = \frac{1}{4}\\ \Leftrightarrow 1 + \sin 2x = \frac{1}{4}\\ \Leftrightarrow \sin 2x = \frac{1}{4} - 1 = - \frac{3}{4}\\ \Rightarrow \sin 2x = - \frac{3}{4}\end{array}\) Chọn A Câu 9 (TH): Phương pháp: - Chia cả tử và mẫu của Q cho \(\cos x\) để làm xuất hiện \(\tan x\). - Thay \(\tan x = 5\) vào tính giá trị của Q. Cách giải: \(\begin{array}{l}Q = \frac{{3\sin x - 4\cos x}}{{\cos x + 2\sin x}}\\ = \frac{{\frac{{3\sin x - 4\cos x}}{{\cos x}}}}{{\frac{{\cos x + 2\sin x}}{{\cos x}}}}\\ = \frac{{3.\frac{{\sin x}}{{\cos x}} - 4.\frac{{\cos x}}{{\cos x}}}}{{\frac{{\cos x}}{{\cos x}} + 2.\frac{{\sin x}}{{\cos x}}}}\\ = \frac{{3\tan x - 4}}{{1 + 2\tan x}}\end{array}\) Thay \(\tan x = 5\) ta được: \(Q = \frac{{3.5 - 4}}{{1 + 2.5}} = 1\) Chọn A Chú ý: Có thể làm cách khác như sau: \(\begin{array}{l}\tan x = 5 \Rightarrow \frac{{\sin x}}{{\cos x}} = 5\\ \Rightarrow \sin x = 5\cos x\\ \Rightarrow Q = \frac{{3\sin x - 4\cos x}}{{\cos x + 2\sin x}}\\ = \frac{{3.5\cos x - 4\cos x}}{{\cos x + 2.5\cos x}}\\ = \frac{{11\cos x}}{{11\cos x}} = 1\end{array}\) Câu 10 (NB): Phương pháp: Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có tiêu cự \(2c\) với \(c = \sqrt {{a^2} - {b^2}} \). Cách giải: \(\begin{array}{l}(E):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\\ \Rightarrow {a^2} = 25,\,\,\,{b^2} = 9\\ \Rightarrow {c^2} = {a^2} - {b^2} = 25 - 9 = 16\\ \Rightarrow c = 4\end{array}\) Vậy tiêu cự là \(2c = 2.4 = 8\). Chọn B Câu 11 (VD): Phương pháp: Gọi \(M\left( {x;y} \right)\) thay và đẳng thức bài cho tìm mối quan hệ giữa \(x\) và \(y\). Từ đó suy ra tập hợp điểm M. Cách giải: Gọi \(M\left( {x;y} \right)\) ta có: \(AM = \sqrt {{{\left( {x - 2} \right)}^2} + {{\left( {y - 0} \right)}^2}} \) \( = \sqrt {{{\left( {x - 2} \right)}^2} + {y^2}} \) \( \Rightarrow M{A^2} = A{M^2} = {\left( {x - 2} \right)^2} + {y^2}\) \(BM = \sqrt {{{\left( {x - 0} \right)}^2} + {{\left( {y - 2} \right)}^2}} \) \( = \sqrt {{x^2} + {{\left( {y - 2} \right)}^2}} \) \( \Rightarrow M{B^2} = B{M^2} = {x^2} + {\left( {y - 2} \right)^2}\) Do đó, \(\begin{array}{l}M{A^2} + M{B^2} = 12\\ \Leftrightarrow {\left( {x - 2} \right)^2} + {y^2}\\ + {x^2} + {\left( {y - 2} \right)^2} = 12\\ \Leftrightarrow {x^2} - 4x + 4 + {y^2}\\ + {x^2} + {y^2} - 4y + 4 = 12\\ \Leftrightarrow 2{x^2} + 2{y^2} - 4x - 4y - 4 = 0\\ \Leftrightarrow {x^2} + {y^2} - 2x - 2y - 2 = 0\end{array}\) Dễ thấy, phương trình trên là phương trình đường tròn có tâm \(I\left( {1;1} \right)\) và bán kính \(R = \sqrt {{1^2} + {1^2} - \left( { - 2} \right)} = 2\). Vậy tập hợp điểm M thỏa mãn \(M{A^2} + M{B^2} = 12\) là đường tròn tâm \(I\left( {1;1} \right)\) và bán kính \(R = 2\). Chọn D Câu 12 (VD): Phương pháp: Bình phương mỗi đẳng thức đã cho và cộng vế với vế các đẳng thức có được. Chú ý: \(\cos \left( {x + y} \right)\) \( = \cos x\cos y - \sin x\sin y\) Cách giải: Ta có: \(\begin{array}{l}\sin x + \sin y = \sqrt 3 \\ \Rightarrow {\left( {\sin x + \sin y} \right)^2} = {\left( {\sqrt 3 } \right)^2}\end{array}\) \( \Rightarrow {\sin ^2}x + 2\sin x\sin y + {\sin ^2}y\)\( = 3\) (1) \(\begin{array}{l}\cos x - \cos y = 1\\ \Rightarrow {\left( {\cos x - \cos y} \right)^2} = {1^2}\end{array}\) \( \Rightarrow {\cos ^2}x - 2\cos x\cos y + {\cos ^2}y\) \( = 1\) (2) Lấy (1) cộng (2) vế với vế ta được:
Chọn B PHẦN II: TỰ LUẬN Câu 1 (VD): Phương pháp: 1. Sử dụng \(\sqrt {f\left( x \right)} = g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\end{array} \right.\) 2. Sử dụng \(\sqrt {f\left( x \right)} \le g\left( x \right) \Leftrightarrow \left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) \ge 0\\f\left( x \right) \le {\left[ {g\left( x \right)} \right]^2}\end{array} \right.\) Cách giải: 1. Giải phương trình \(\sqrt {{x^2} - 2x + 6} = 2x - 1\). Ta có: \(\sqrt {{x^2} - 2x + 6} = 2x - 1\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}2x - 1 \ge 0\\{x^2} - 2x + 6 = {\left( {2x - 1} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{2}\\{x^2} - 2x + 6 = 4{x^2} - 4x + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{2}\\3{x^2} - 2x - 5 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \frac{1}{2}\\\left[ \begin{array}{l}x = - 1\\x = \frac{5}{3}\end{array} \right.\end{array} \right.\\ \Rightarrow x = \frac{5}{3}\end{array}\) Vậy phương trình có nghiệm \(x = \frac{5}{3}.\) 2. Giải bất phương trình \(\sqrt { - {x^2} + 3x + 4} \le x + 1\). Ta có: \(\sqrt { - {x^2} + 3x + 4} \le x + 1\) \(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\ - {x^2} + 3x + 4 \ge 0\\ - {x^2} + 3x + 4 \le {\left( {x + 1} \right)^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\ - \left( {x + 1} \right)\left( {x - 4} \right) \ge 0\\ - {x^2} + 3x + 4 \le {x^2} + 2x + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\\left( {x + 1} \right)\left( {x - 4} \right) \le 0\\2{x^2} - x - 3 \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge 1\\ - 1 \le x \le 4\\\left( {2x - 3} \right)\left( {x + 1} \right) \ge 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}1 \le x \le 4\\\left[ \begin{array}{l}x \ge \frac{3}{2}\\x \le - 1\end{array} \right.\end{array} \right.\\ \Rightarrow \frac{3}{2} \le x \le 4\end{array}\) Vậy bất phương trình có tập nghiệm \(S = \left[ {\frac{3}{2};4} \right]\) Câu 2 (VD): Phương pháp: 1. Sử dụng \(1 + {\tan ^2}a = \frac{1}{{{{\cos }^2}a}};\) \(\cos 2a = 2{\cos ^2}a - 1\) 2. Sử dụng \(A + B + C = {180^0};\) \(\sin \alpha = \sin \left( {{{180}^0} - \alpha } \right);\) \(\cos \alpha = \cos \left( { - \alpha } \right);\) \(\cos \alpha = \sin \left( {{{90}^0} - \alpha } \right)\). Cách giải: 1. Cho biết \(\frac{\pi }{2} < a < \pi \) và \(\tan a = - 2\). Tính \(\cos a\) và \(\cos 2a\). Ta có: \(\begin{array}{l}1 + {\tan ^2}a = \frac{1}{{{{\cos }^2}a}}\\ \Leftrightarrow 1 + {\left( { - 2} \right)^2} = \frac{1}{{{{\cos }^2}a}}\\ \Leftrightarrow \frac{1}{{{{\cos }^2}a}} = 5\\ \Leftrightarrow {\cos ^2}a = \frac{1}{5}\end{array}\) \( \Rightarrow \cos a = - \frac{1}{{\sqrt 5 }}\) (vì \(\frac{\pi }{2} < a < \pi \)) Lại có: \(\cos 2a = 2{\cos ^2}a - 1\) \( = 2.{\left( { - \frac{1}{{\sqrt 5 }}} \right)^2} - 1\) \( = \frac{2}{5} - 1 = \frac{{ - 3}}{5}\) Vậy \(\cos a = - \frac{1}{{\sqrt 5 }};\) \(\cos 2a = \frac{{ - 3}}{5}\). 2. Cho tam giác \(ABC\). Chứng minh rằng \(\sin 2A + \sin 2B + \sin 2C\)\( = 4\sin A\sin B\sin C\). Ta có: \(\sin 2A + \sin 2B + \sin 2C\) \(\begin{array}{l} = 2\sin \frac{{2A + 2B}}{2}\cos \frac{{2A - 2B}}{2} + \sin 2C\\ = 2\sin \left( {A + B} \right)\cos \left( {A - B} \right) + 2\sin C\cos C\end{array}\) \( = 2\sin \left( {{{180}^0} - \left( {A + B} \right)} \right)\cos \left( {A - B} \right)\)\( + 2\sin C\cos C\) \( = 2\sin C.\cos \left( {A - B} \right)\) \( + 2\sin C\cos C\) \( = 2\sin C\left( {\cos \left( {A - B} \right) + \cos C} \right)\) \( = 2\sin C.2\cos \frac{{A - B + C}}{2}.\cos \frac{{A - B - C}}{2}\) \( = 4\sin C.\cos \frac{{A + C - B}}{2}.\cos \frac{{B + C - A}}{2}\) Ta có: \(\cos \frac{{A + C - B}}{2} = \sin \left( {{{90}^0} - \frac{{A + C - B}}{2}} \right)\) \( = \sin \left( {\frac{{A + B + C}}{2} - \frac{{A + C - B}}{2}} \right)\)\( = \sin B\) (do \(A + B + C = {180^0}\) ) \(\cos \frac{{B + C - A}}{2} = \sin \left( {{{90}^0} - \frac{{B + C - A}}{2}} \right)\) \( = \sin \left( {\frac{{A + B + C}}{2} - \frac{{B + C - A}}{2}} \right)\)\( = \sin A\) (do \(A + B + C = {180^0}\) ) Từ đó ta có: \(4\sin C.\cos \frac{{A + C - B}}{2}.\cos \frac{{B + C - A}}{2}\)\( = 4\sin A\sin B\sin C\) Hay \(\sin 2A + \sin 2B + \sin 2C = 4\sin A\sin B\sin C\). Câu 3 (VD): Phương pháp: 1. a) Viết phương trình tiếp tuyến đi qua \(A\) và vuông góc với \(AI\) (\(I\) là tâm đường tròn \(\left( C \right)\)) Đường thẳng đi qua \(M\left( {{x_0};{y_0}} \right)\) và có 1 VTPT \(\overrightarrow n = \left( {a;b} \right)\left( {{a^2} + {b^2} \ne 0} \right)\) có phương trình: \(a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0\) b) Xác định được phương trình đường thẳng \(\Delta :3x - 4y + c = 0\left( {c \ne - 2} \right)\) Sử dụng công thức tính khoảng cách từ \(M\left( {{x_0};{y_0}} \right)\) đến đường thẳng \(\Delta :ax + by + c = 0\) là: \(d\left( {M;\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\) 2. Sử dụng Elip \(\left( E \right):\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) có \({b^2} + {c^2} = {a^2}\) và hai tiêu điểm \({F_1}\left( { - c;0} \right),{F_2}\left( {c;0} \right)\) Với \(M \in \left( E \right)\) thì \(M{F_1} + M{F_2} = 2a.\) Cách giải: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): \({x^2} + {y^2} - 6x + 4y - 12 = 0\). a) Viết phương trình tiếp tuyến của đường tròn (C) tại điểm \(A( - 1;1)\). Xét đường tròn \({x^2} + {y^2} - 6x + 4y - 12 = 0\) có tâm \(I\left( {3; - 2} \right)\) và bán kính \(R = \sqrt {{3^2} + {{\left( { - 2} \right)}^2} - \left( { - 12} \right)} \) \( = 5\) Tiếp tuyến tại điểm \(A\left( { - 1;1} \right)\) vuông góc với \(AI\) nên nhận \(\overrightarrow {AI} = \left( {4; - 3} \right)\) làm véc tơ pháp tuyến Phương trình tiếp tuyến cần tìm là: \(4\left( {x + 1} \right) - 3\left( {y - 1} \right) = 0\) \( \Leftrightarrow 4x - 3y + 7 = 0\) b) Viết phương trình đường thẳng \(\Delta \) song song với đường thẳng \(d:3x - 4y - 2 = 0\) và cắt đường tròn (C) tại hai điểm \(A,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} B\) sao cho độ dài đoạn thẳng \(AB = 8\).
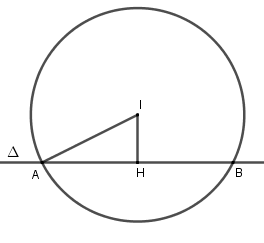
Vì \(\Delta //d:3x - 4y - 2 = 0\) nên phương trình đường thẳng \(\Delta :3x - 4y + c = 0\left( {c \ne - 2} \right)\) Gọi \(H\) là trung điểm của dây \(AB \Rightarrow IH \bot AB\) Ta có: \(IA = R = 5;\) \(HA = \frac{{AB}}{2} = 4\) Xét tam giác vuông \(AIH\), theo định lý Pytago ta có: \(IH = \sqrt {I{A^2} - A{H^2}} \) \( = \sqrt {{5^2} - {4^2}} = 3\) Suy ra \(d\left( {I;\Delta } \right) = 3\) \(\begin{array}{l} \Leftrightarrow \frac{{\left| {3.3 - 4.\left( { - 2} \right) + c} \right|}}{{\sqrt {{3^2} + {{\left( { - 4} \right)}^2}} }} = 3\\ \Leftrightarrow \frac{{\left| {17 + c} \right|}}{5} = 3\\ \Leftrightarrow \left| {17 + c} \right| = 15\\ \Leftrightarrow \left[ \begin{array}{l}17 + c = 15\\17 + c = - 15\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}c = - 2\left( {ktm} \right)\\c = - 32\left( {tm} \right)\end{array} \right.\end{array}\) Vậy phương trình đường thẳng \(\Delta :3x - 4y - 32 = 0\). 2. Trong mặt phẳng tọa độ Oxy, cho elip \((E):\;\;\frac{{{x^2}}}{4} + {y^2} = 1\). Gọi \({F_1},{F_2}\) là hai tiêu điểm của \((E)\) và điểm \(M \in (E)\) sao cho \(M{F_1} \bot M{F_2}\). Tính \(MF_1^2 + MF_2^2\) và diện tích \(\Delta \;M{F_1}{F_2}\). Xét \((E):\;\;\frac{{{x^2}}}{4} + {y^2} = 1\) có \(a = 2;b = 1\) \( \Rightarrow {c^2} = {a^2} - {b^2}\) \( = 4 - 1 = 3\) \( \Rightarrow c = \sqrt 3 \) Hai tiêu điểm của \(\left( E \right)\) là \({F_1}\left( { - \sqrt 3 ;0} \right),{F_2}\left( {\sqrt 3 ;0} \right)\) \( \Rightarrow {F_1}{F_2} = 2\sqrt 3 \) Xét \(\Delta {F_1}M{F_2}\) vuông tại \(M\) (do \(M{F_1} \bot M{F_2}\)), theo định lý Pytago ta có: \(MF_1^2 + MF_2^2 = {F_1}F_2^2\) \(\begin{array}{l} \Leftrightarrow MF_1^2 + MF_2^2 = {\left( {2\sqrt 3 } \right)^2}\\ \Leftrightarrow MF_1^2 + MF_2^2 = 12\end{array}\) Ta có: \(M{F_1} + M{F_2} = 2a = 4\) và \(MF_1^2 + MF_2^2 = 12\) Do đó: \(\begin{array}{l}{\left( {M{F_1} + M{F_2}} \right)^2} = 16\\ \Leftrightarrow MF_1^2 + MF_2^2 + 2M{F_1}.M{F_2} = 16\\ \Leftrightarrow 12 + 2.M{F_1}.M{F_2} = 16\\ \Leftrightarrow M{F_1}.M{F_2} = 2\end{array}\) Vì tam giác \(M{F_1}{F_2}\) vuông tại \(M\) nên \({S_{M{F_1}{F_2}}} = \frac{1}{2}M{F_1}.M{F_2}\) \( = \frac{1}{2}.2 = 1\) (đơn vị diện tích) Câu 4 (VDC): Cho tam giác \(ABC\) có số đo ba góc là \(A,B,C\) thỏa mãn điều kiện \(\tan \frac{A}{2} + \tan \frac{B}{2} + \tan \frac{C}{2} = \sqrt 3 \). Chứng minh rằng tam giác \(ABC\) là tam giác đều. Phương pháp: - Chứng minh \(\tan \frac{A}{2}\tan \frac{B}{2} + \tan \frac{B}{2}\tan \frac{C}{2}\) \( + \tan \frac{C}{2}\tan \frac{A}{2} = 1\) - Chứng minh và sử dụng bất đẳng thức \({\left( {a + b + c} \right)^2} \ge 3\left( {ab + bc + ca} \right)\) Cách giải: *) Trước hết ta chứng minh: \(\tan \frac{A}{2}\tan \frac{B}{2} + \tan \frac{B}{2}\tan \frac{C}{2}\) \( + \tan \frac{C}{2}\tan \frac{A}{2} = 1\) Ta có: \(\begin{array}{l}A + B + C = \pi \Rightarrow \frac{{A + B + C}}{2} = \frac{\pi }{2}\\ \Rightarrow \frac{{A + B}}{2} = \frac{\pi }{2} - \frac{C}{2}\\ \Rightarrow \tan \frac{{A + B}}{2} = \tan \left( {\frac{\pi }{2} - \frac{C}{2}} \right)\\ \Leftrightarrow \tan \left( {\frac{A}{2} + \frac{B}{2}} \right) = \cot \frac{C}{2}\\ \Leftrightarrow \frac{{\tan \frac{A}{2} + \tan \frac{B}{2}}}{{1 - \tan \frac{A}{2}\tan \frac{B}{2}}} = \frac{1}{{\tan \frac{C}{2}}}\end{array}\) \(\begin{array}{l} \Leftrightarrow \left( {\tan \frac{A}{2} + \tan \frac{B}{2}} \right)\tan \frac{C}{2}\\ = 1 - \tan \frac{A}{2}\tan \frac{B}{2}\\ \Leftrightarrow \tan \frac{A}{2}\tan \frac{C}{2} + \tan \frac{B}{2}\tan \frac{C}{2}\\ = 1 - \tan \frac{A}{2}\tan \frac{B}{2}\\ \Leftrightarrow \tan \frac{A}{2}\tan \frac{B}{2} + \tan \frac{B}{2}\tan \frac{C}{2}\\ + \tan \frac{C}{2}\tan \frac{A}{2} = 1\end{array}\) *) Chứng minh bất đẳng thức \({\left( {a + b + c} \right)^2} \ge 3\left( {ab + bc + ca} \right)\) Ta có: \(\begin{array}{l}{\left( {a + b + c} \right)^2} \ge 3\left( {ab + bc + ca} \right)\\ \Leftrightarrow {a^2} + {b^2} + {c^2} + 2ab + 2bc + 2ca\\ \ge 3ab + 3bc + 3ca\\ \Leftrightarrow {a^2} + {b^2} + {c^2} - ab - bc - ca \ge 0\\ \Leftrightarrow 2{a^2} + 2{b^2} + 2{c^2} - 2ab - 2bc - 2ca \ge 0\\ \Leftrightarrow \left( {{a^2} - 2ab + {b^2}} \right) + \left( {{b^2} - 2bc + {c^2}} \right)\\ + \left( {{c^2} - 2ca + {a^2}} \right) \ge 0\\ \Leftrightarrow {\left( {a - b} \right)^2} + {\left( {b - c} \right)^2} + {\left( {c - a} \right)^2} \ge 0\end{array}\) (BĐT cuối luôn đúng do \(\left\{ \begin{array}{l}{\left( {a - b} \right)^2} \ge 0\\{\left( {b - c} \right)^2} \ge 0\\{\left( {c - a} \right)^2} \ge 0\end{array} \right.\)) Áp dụng bđt vừa chứng minh với \(a = \tan \frac{A}{2},b = \tan \frac{B}{2},\) \(c = \tan \frac{C}{2}\) ta được: \(\begin{array}{l}{\left( {\tan \frac{A}{2} + \tan \frac{B}{2} + \tan \frac{C}{2}} \right)^2}\\ \ge 3\left( {\tan \frac{A}{2}\tan \frac{B}{2} + \tan \frac{B}{2}\tan \frac{C}{2} + \tan \frac{C}{2}\tan \frac{A}{2}} \right)\\ = 3.1 = 3\\ \Rightarrow {\left( {\tan \frac{A}{2} + \tan \frac{B}{2} + \tan \frac{C}{2}} \right)^2} \ge 3\\ \Rightarrow \tan \frac{A}{2} + \tan \frac{B}{2} + \tan \frac{C}{2} \ge \sqrt 3 \end{array}\) Đẳng thức xảy ra khi \(\tan \frac{A}{2} = \tan \frac{B}{2} = \tan \frac{C}{2}\) hay \(A = B = C = \frac{\pi }{3}\). Vậy tam giác ABC đều (đpcm). Loigiaihay.com
|














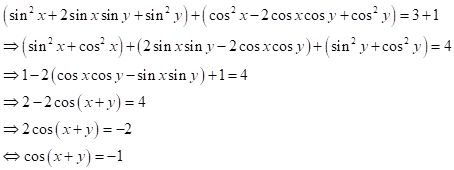






Danh sách bình luận