Giải đề thi học kì 2 toán lớp 10 năm 2019 - 2020 trường THPT Phú Lương - Thái Nguyên

Đề bài

Phần I. Trắc nghiệm (6 điểm)

Câu 1. Tìm điều kiện xác định của bất phương trình sau:$\dfrac{{1 - x}}{{{x^2} + 1}} > \dfrac{1}{{x + 1}}$.

A.$\forall x \in \mathbb{R}$             B. $x \ne  \pm 1$

C. $x \ne 1$                D. $x \ne  - 1$

Câu 2. Bảng xét dấu sau là của nhị thức nào trong các nhị thức đã cho?

A.$f(x) = 3x + 6$ 

B. $f(x) = 4 - 2x$

C. $f(x) =  - 2x - 4$

D. $f(x) = 6 - 3x$

Câu 3. Cho tam thức bậc hai $f(x) = a{x^2} + bx + c,a \ne 0,$$\Delta  = {b^2} - 4ac$. Mệnh đề nào sau đây đúng?

A. Tam thức luôn cùng dấu với $a$ khi $\Delta  = 0$.

B. Tam thức luôn cùng dấu với $a$khi $\Delta  < 0$.

C. Tam thức luôn cùng dấu với $a$khi $\Delta  \le 0$.

D. Tam thức luôn cùng dấu với $a$ khi $\Delta  > 0$.

Câu 4.Trên đường tròn lượng giác điểm M biểu diễn cung $\dfrac{{5\pi }}{6} + k2\pi ,k \in Z$. M ở góc phần tư nào ?

A. I.                             B. II.

C. III.                          D. IV.

Câu 5. Trong các công thức sau công thức nào sai?

A. $\sin (a - b) = \sin a.\cos b - \cos a.\sin b$

B. $\sin (a + b) = \sin a.\cos b + \cos a.\sin b$

C. $\cos (a + b) = \cos a.\cos b + \sin a.\sin b$

C. $\cos (a - b) = \cos a.\cos b + \sin a.\sin b$

Câu 6. Véc tơ nào sau đây là một véc tơ pháp tuyến của đường thẳng $2x - y + 3 = 0$?

A. $\overrightarrow u ( - 2;1)$.                     B. $\overrightarrow n (2;1)$

C. $\overrightarrow a (1; - 2)$                       D. $\overrightarrow b ( - 1;2)$

Câu 7.  Đường thẳng $\Delta$ có véc tơ chỉ phương $\overrightarrow u (2; - 3)$. Mệnh đề nào sau đây đúng?

A. $m = \dfrac{{ - 2}}{3}$ là hệ số góc của $\Delta$

B. $\overrightarrow b (3;2)$ là một véc tơ pháp tuyến của$\Delta$

C.$m = \dfrac{3}{2}$ là hệ số góc của $\Delta$

D. $\overrightarrow n (2;3)$ là một véc tơ pháp tuyến của $\Delta$

Câu 8. Trong các điểm sau, điểm nào  thuộc đường thẳng $\left\{ \begin{array}{l}x = 1 + t\\y = 2 - t\end{array} \right.$

A. $A(2;3)$                B. $B(3;1)$

C. $C(1; - 2)$             D. $A(0;3)$

Câu 9. Tính khoảng cách từ điểm $A( - 2;3)$ đến đường thẳng $4x - 3y - 3 = 0$ ta được kết quả.

A. $d = 2$                  B. $d = 4$

C. $d =  - 5$               D. $d = \dfrac{{20}}{{\sqrt {13} }}$

Câu 10. Xác định tọa độ tâm I của đường tròn có phương trình: ${x^2} + {y^2} + 4x - 6y - 1 = 0$.

A. $I( - 2;3)$              B. $I(4; - 6)$

C. $I(2; - 3)$              D. $I( - 4;6)$

Câu 11. Tam thức bậc hai $f(x) = {x^2} - 3x$ nhận giá trị âm trên khoảng nào?

A. $( - \infty ;0)$                    B. $( - 1;3)$

C. $(1;3)$                   D. $(3; + \infty )$

Câu 12. Tập nghiệm của bất phương trình  $\dfrac{{x - 1}}{{3 - x}} \ge 0$là.

A. $(1;3)$                   B. $[1;3)$

C. $[1;3]$                   D.$(1;3]$

 Câu 13. Tính$\sin a$ biết $\cos a =  - \dfrac{1}{3}$và $\dfrac{\pi }{2} < a < \pi$

A. $\sin a = \dfrac{{2\sqrt 2 }}{3}$

B.  $\sin a =  - \dfrac{{2\sqrt 2 }}{3}$

C. $\sin a =  - \dfrac{{\sqrt {10} }}{3}$

D. $\sin a = \dfrac{{\sqrt {10} }}{3}$

Câu 14. Cho$\tan a = 2$ tính giá trị $A = \dfrac{1}{{{{\cos }^2}a}} + \dfrac{{\cos a + \sin a}}{{\cos a - \sin a}} - 5$ 

A.  $A = 5$                B. $A = 4$

C. $A =  - 3$              D. $A =  - 2$

Câu 15. Biến tổng sau thành tích $B = \sin a + \cos 2a - \sin 3a$ được kết quả

A. $\cos 2a(1 - 2\cos a)$  

B. $\cos 2a(1 + 2\sin a)$       

C. $- \cos 2a(2\cos a + 1)$

D. $\cos 2a(1 - 2\sin a)$

Câu 16.Phương trình tổng quát của đường thẳng$\left\{ \begin{array}{l}x = t\\y = 2 + t\end{array} \right.$ là:

A. $x + y - 2 = 0$

B. $x - y + 2 = 0$

C. $x - y - 2 = 0$

D. $x + y + 2 = 0$

Câu 17. Vị trí tương đối của hai đường thẳng ${\Delta _1}:2x + y + 3 = 0;$${\Delta _2}:x + 2y + 3 = 0$ là:

A. Vuông góc.

B. Cắt nhau nhưng không vuông góc.

C. Song song.

D.Trùng nhau .

Câu 18. Tính cosin của góc giữa hai đường thẳng ${\Delta _1}:x - y + 3 = 0;$${\Delta _2}:3x + 4y + 3 = 0$

A. $\cos ({\Delta _1},{\Delta _2}) =  - \dfrac{{\sqrt 2 }}{{10}}$

B. $\cos ({\Delta _1},{\Delta _2}) =  - \dfrac{{\sqrt 5 }}{{10}}$

C. $\cos ({\Delta _1},{\Delta _2}) = \dfrac{{\sqrt 2 }}{{10}}$

D. $\cos ({\Delta _1},{\Delta _2}) = \dfrac{{\sqrt 5 }}{{10}}$

Câu 19.Viết phương trình đường tròn tâm $I(2; - 1)$ và tiếp xúc với đường thẳng $\Delta :4x - 3y - 1 = 0$.

A. ${(x - 2)^2} + {(y + 1)^2} = 1$

B. ${(x + 2)^2} + {(y - 1)^2} = 1$   

C. ${(x - 2)^2} + {(y + 1)^2} = 2$

D. ${(x - 2)^2} + {(y + 1)^2} = 4$

Câu 20.Cho tam giác $ABC$ mệnh đề nào sau đây sai?

A. $\sin (A + B) =  - \sin C$

B. $\cos (A + B) =  - \cos C$

C. $\sin \dfrac{{A + B}}{2} = \cos \dfrac{C}{2}$

D. $\tan \dfrac{{A + B}}{2} = \cot \dfrac{C}{2}$

Câu 21. Rút gọn biểu thức $M = 2{\cos ^2}(\dfrac{\pi }{2} - \dfrac{a}{2}) + \sqrt 2 \sin (\dfrac{\pi }{4} + a) - 1$

A. $M = \sin a$

B. $M =  - \sin a$

C. $M = \cos a$

D. $M =  - \cos a$

Câu 22. Đường thẳng nào sau đây đi qua điểm $M(0;2)$ và vuông góc với đường thẳng $\left\{ \begin{array}{l}x = 1 - t\\y = 2 + t\end{array} \right.$.

A. $\left\{ \begin{array}{l}x =  - t\\y = 2 + t\end{array} \right.$

B. $\left\{ \begin{array}{l}x =  - t\\y = t\end{array} \right.$

C. $\left\{ \begin{array}{l}x = t\\y = 2 - t\end{array} \right.$

D. $\left\{ \begin{array}{l}x = t\\y = 2 + t\end{array} \right.$

Câu 23. Có bao nhiêu số nguyên $m$ để tam thức $f(x) =  - {x^2} + 2(m + 2)x + 9m - 4$ luôn âm trên $\mathbb{R}$.

A.0                              B.13

C.12                            D. vô số

Câu 24. Tìm trên đường tròn ${(x - 3)^2} + {(y - 3)^2} = 9$ điểm M sao cho M cách đường thẳng $y =  - 2$khoảng lớn nhất.

A. $M(0;3)$                B. $M(3;6)$

C. $M(1;\sqrt 5  + 3)$            D. $M(4;7)$

Phần 2. Tự luận (4 điểm)

Bài 1. Giải bất phương trình: $x + \sqrt {x - 1}  > \sqrt {x - 1}  - 2$

Bài 2. Cho $\sin a =  - \dfrac{2}{3}$. Tính $9.\cos 2a$

Bài 3. Cho hai điểm $A(1;2),B(3;4)$.

a) Viết phương trình tổng quát của đường thẳng qua A và vuông góc với AB

b) Viết phương trình đường tròn đường kính AB

Bài 4.Tìm $m$để phương trình  $m{x^2} + 2(m - 1)x - 4 = 0$ có hai nghiệm phân biệt

Bài 5. Chứng minh rằng tam giác ABC vuông nếu: $\cot \dfrac{B}{2} = \dfrac{{a + c}}{b}$

Lời giải chi tiết

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

 PHẦN TRẮC NGHIỆM

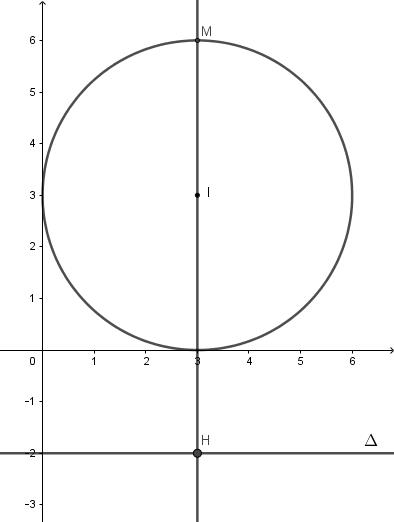
 Câu 1 (TH):

Phương pháp:

Sử dụng phân thức $\dfrac{{A\left( x \right)}}{{B\left( x \right)}}$ xác định khi $B\left( x \right) \ne 0$

Cách giải:

Điều kiện xác định: $\left\{ \begin{array}{l}{x^2} + 1 \ne 0\\x + 1 \ne 0\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}{x^2} \ne  - 1\left( {ld} \right)\\x \ne  - 1\end{array} \right.$ $\Rightarrow x \ne  - 1$

Chọn D

Câu 2 (TH):

Phương pháp:

Sử dụng qui tắc xét dấu của nhị thức $f\left( x \right) = ax + b$ $\left( {a \ne 0} \right)$

+) $a.f\left( x \right) > 0$ với $x > \dfrac{{ - b}}{a}$

+) $a.f\left( x \right) < 0$ với $x <  - \dfrac{b}{a}$

Cách giải:

Từ bảng xét dấu ta thấy nhị thức $f\left( x \right) = ax + b$ có nghiệm $x =  - 2$ và có hệ số $a < 0$ nên trong các đáp án chỉ có đáp án C với $f\left( x \right) =  - 2x - 4$ thỏa mãn (vì có hệ số $a =  - 2 < 0$ và $- 2x - 4 = 0$ $\Leftrightarrow x =  - 2$).

Chọn C

Câu 3 (NB):

Phương pháp:

Sử dụng qui tắc xét dấu của tam thức bậc hai $f\left( x \right) = a{x^2} + bx + c$  $\left( {a \ne 0} \right)$

Nếu $\Delta  < 0$ thì $a.f\left( x \right) > 0$

Cách giải:

Tam thức luôn cùng dấu với $a$khi $\Delta  < 0$ là khẳng định đúng.

Chọn B

Câu 4 (NB):

Phương pháp:

Với $\dfrac{\pi }{2} < \alpha  < \pi$ thì điểm M biểu diễn cung $\alpha  + k2\pi ,k \in \mathbb{Z}$ thuộc góc phần tư thứ hai

Cách giải:

Vì $\dfrac{\pi }{2} < \dfrac{{5\pi }}{6} < \pi$ nên điểm M biểu diễn cung $\dfrac{{5\pi }}{6} + k2\pi ,k \in Z$ thuộc góc phần tư thứ hai.

Chọn B

Câu 5 (NB):

Phương pháp:

Sử dụng các công thức lượng giác:

$\begin{array}{l}\sin \left( {a \pm b} \right) = \sin a\cos b \pm \cos a\sin b\\\cos \left( {a \pm b} \right) = \cos a\cos b \mp \sin a\sin b\end{array}$

Cách giải:

Ta có: $\cos \left( {a + b} \right) = \cos a\cos b - \sin a\sin b$ nên C sai.

Chọn C

Câu 6 (NB):

Phương pháp:

Đường thẳng $ax + by + c = 0$ có 1 VTPT là $\overrightarrow n  = \left( {a;b} \right)$

Cách giải:

Đường thẳng $2x - y + 3 = 0$ có 1 VTPT là $\overrightarrow n  = \left( {2; - 1} \right)$

Suy ra $\overrightarrow u  = \left( { - 2;1} \right)$ cũng là 1 VTPT của đường thẳng $2x - y + 3 = 0$.

Chọn A

Câu 7 (TH):

Phương pháp:

Đường thẳng $\Delta$ có VTCP là $\overrightarrow u  = \left( {a;b} \right)$ $\left( {a;b \ne 0} \right)$ thì có hệ số góc $k = \dfrac{b}{a}$ và có VTPT $\overrightarrow n  = \left( { - b;a} \right)$

Cách giải:

Ta có: $\overrightarrow u  = \left( {2; - 3} \right)$ là VTCP của $\Delta$ nên đường thẳng $\Delta$ có hệ số góc $k =  - \dfrac{3}{2}$ và VTPT $\overrightarrow n  = \left( {3;2} \right)$

Chọn B

Câu 8 (TH):

Phương pháp:

Thay tọa độ từng điểm vào phương trình đường thẳng để chọn ra điểm thuộc đường thẳng đó.

Cách giải:

+) Với $A\left( {2;3} \right)$ ta có: $\left\{ \begin{array}{l}2 = 1 + t\\3 = 2 - t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 1\\t =  - 1\end{array} \right.$ (vô lý) nên loại A

+) Với $B\left( {3;1} \right)$ ta có: $\left\{ \begin{array}{l}3 = 1 + t\\1 = 2 - t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 2\\t = 1\end{array} \right.$ (vô lý) nên loại B

+) Với $C\left( {1; - 2} \right)$ ta có: $\left\{ \begin{array}{l}1 = 1 + t\\ - 2 = 2 - t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = 0\\t = 4\end{array} \right.$ (vô lý) nên loại C

+) Với $A\left( {0;3} \right)$ ta có: $\left\{ \begin{array}{l}0 = 1 + t\\3 = 2 - t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t =  - 1\\t =  - 1\end{array} \right.$ (thỏa mãn) nên $A\left( {0;3} \right)$ thuộc đường thẳng đã cho

Chọn D

Câu 9 (TH):

Phương pháp:

Sử dụng công thức tính khoảng cách từ $M\left( {{x_0};{y_0}} \right)$ đến đường thẳng $\Delta :ax + by + c = 0$ là:

$d\left( {M;\Delta } \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$

Cách giải:

Gọi đường thẳng $\Delta :4x - 3y - 3 = 0$

Khoảng cách cần tìm là: $d\left( {A;\Delta } \right) = \dfrac{{\left| {4.\left( { - 2} \right) - 3.3 - 3} \right|}}{{\sqrt {{4^2} + {{\left( { - 3} \right)}^2}} }} = 4$

Chọn B

Câu 10 (TH):

Phương pháp:

Đường tròn $\left( C \right):{x^2} + {y^2} - 2ax - 2by + c = 0$ có tâm $I\left( {a;b} \right)$  

Cách giải:

Tâm $I$ của đường tròn có phương trình: ${x^2} + {y^2} + 4x - 6y - 1 = 0$ là $I\left( {\dfrac{4}{{ - 2}};\dfrac{{ - 6}}{{ - 2}}} \right)$  hay $I\left( { - 2;3} \right)$

Chọn A

Câu 11 (TH):

Phương pháp:

Sử dụng định lý dấu của tam thức bậc hai $f\left( x \right) = a{x^2} + bx + c$ có hai nghiệm ${x_1} < {x_2}$

Nếu ${x_1} < x < {x_2}$ thì $a.f\left( x \right) < 0$

Nếu $\left[ \begin{array}{l}x < {x_1}\\x > {x_2}\end{array} \right.$  thì $a.f\left( x \right) > 0$ 

Cách giải:

Đa thức $f\left( x \right) = {x^2} - 3x$ có hai nghiệm $x = 0;x = 3$

Ta có bảng xét dấu:

 

Từ bảng xét dấu ta có $f\left( x \right) < 0 \Leftrightarrow 0 < x < 3$

Như vậy tam thức đã cho có giá trị âm trên khoảng $\left( {0;3} \right)$ nên nó có giá trị âm trên $\left( {1;3} \right)$

Chọn C

Câu 12 (TH):

Phương pháp:

Sử dụng $\dfrac{{A\left( x \right)}}{{B\left( x \right)}} \ge 0$ $\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}A\left( x \right) \ge 0\\B\left( x \right) > 0\end{array} \right.\\\left\{ \begin{array}{l}A\left( x \right) \le 0\\B\left( x \right) < 0\end{array} \right.\end{array} \right.$

Cách giải:

Ta có: $\dfrac{{x - 1}}{{3 - x}} \ge 0$

$\Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x - 1 \ge 0\\3 - x > 0\end{array} \right.\\\left\{ \begin{array}{l}x - 1 \le 0\\3 - x < 0\end{array} \right.\end{array} \right.$

$\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x \ge 1\\x < 3\end{array} \right.\\\left\{ \begin{array}{l}x \le 1\\x > 3\end{array} \right.\left( {VN} \right)\end{array} \right.\\ \Rightarrow 1 \le x < 3\end{array}$

Vậy bất phương trình có tập nghiệm $S = \left[ {1;3} \right)$

Chọn B

Câu 13 (TH):

Phương pháp:

Sử dụng ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$

Cách giải:

Ta có: ${\sin ^2}\alpha  + {\cos ^2}\alpha  = 1$

$\begin{array}{l} \Leftrightarrow {\sin ^2}\alpha  + {\left( { - \dfrac{1}{3}} \right)^2} = 1\\ \Leftrightarrow {\sin ^2}\alpha  = \dfrac{8}{9}\end{array}$

$\Rightarrow \sin \alpha  = \dfrac{{2\sqrt 2 }}{3}$  (do $\dfrac{\pi }{2} < a < \pi$)

Chọn A

Câu 14 (TH):

Phương pháp:

Sử dụng công thức $1 + {\tan ^2}\alpha  = \dfrac{1}{{{{\cos }^2}\alpha }}$

Cách giải:

Vì $\tan \alpha  = 2 \Rightarrow \cos \alpha  \ne 0$, ta có:

$A = \dfrac{1}{{{{\cos }^2}a}} + \dfrac{{\cos a + \sin a}}{{\cos a - \sin a}} - 5$

$= 1 + {\tan ^2}\alpha  + \dfrac{{\dfrac{{\cos \alpha }}{{\cos \alpha }} + \dfrac{{\sin \alpha }}{{\cos \alpha }}}}{{\dfrac{{\cos \alpha }}{{\cos \alpha }} - \dfrac{{\sin \alpha }}{{\cos \alpha }}}} - 5$

$= 1 + {\tan ^2}\alpha  + \dfrac{{1 + \tan \alpha }}{{1 - \tan \alpha }} - 5$

$= 1 + {2^2} + \dfrac{{1 + 2}}{{1 - 2}} - 5 =  - 3$

Chọn C

Câu 14 (TH):

Phương pháp:

Sử dụng công thức $\sin a - \sin b = 2\cos \dfrac{{a + b}}{2}\sin \dfrac{{a - b}}{2}$

Cách giải:

Ta có:

$B = \sin a + \cos 2a - \sin 3a$

$\begin{array}{l} = \left( {\sin a - \sin 3a} \right) + \cos 2a\\ = 2\cos \dfrac{{a + 3a}}{2}.\sin \dfrac{{a - 3a}}{2} + \cos 2a\\ = 2\cos 2a.\sin \left( { - a} \right) + \cos 2a\\ =  - 2\cos 2a\sin a + \cos 2a\\ = \cos 2a\left( {1 - 2\sin a} \right)\end{array}$

Chọn D

Câu 16 (TH):

Phương pháp:

Rút $t$ theo $x;y$, từ đó suy ra phương trình tổng quát

Cách giải:

Ta có: $\left\{ \begin{array}{l}x = t\\y = 2 + t\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}t = x\\t = y - 2\end{array} \right.$$\Rightarrow x = y - 2 \Leftrightarrow x - y + 2 = 0$

Vậy phương trình tổng quát của đường thẳng đã cho là $x - y + 2 = 0$

Chọn B

Câu 17 (TH):

Phương pháp:

Sử dụng: Đường thẳng $\Delta :ax + by + c = 0$ và đường thẳng ${\Delta _1}:a'x + b'y + c = 0$ cắt nhau $\Leftrightarrow \dfrac{a}{{a'}} \ne \dfrac{b}{{b'}}\left( {a';b' \ne 0} \right)$

Cách giải:

Đường thẳng ${\Delta _1}$ có VTPT $\overrightarrow {{n_1}}  = \left( {2;1} \right)$

Đường thẳng ${\Delta _2}$ có VTPT $\overrightarrow {{n_2}}  = \left( {1;2} \right)$

Vì $\dfrac{2}{1} \ne \dfrac{1}{2}$ nên ${\Delta _1}$ và ${\Delta _2}$ cắt nhau.

Lại có $\overrightarrow {{n_1}} .\overrightarrow {{n_2}}$ $= 2.1 + 1.2 = 4 \ne 0$ nên ${\Delta _1}$ và ${\Delta _2}$ không vuông góc.

Chọn B

Câu 18 (TH):

Phương pháp:

Góc giữa đường thẳng $\Delta :ax + by + c = 0$ và đường thẳng ${\Delta _1}:a'x + b'y + c = 0$ là $\alpha$ thỏa mãn $\cos \alpha  = \dfrac{{\left| {a.a' + b.b'} \right|}}{{\sqrt {{a^2} + {b^2}} .\sqrt {a{'^2}}  + b{'^2}}}$

Cách giải:

Gọi góc giữa hai đường thẳng ${\Delta _1};{\Delta _2}$ là $\alpha$, ta có:

$\cos \alpha  = \dfrac{{\left| {1.3 + \left( { - 1} \right).4} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{3^2} + {4^2}} }}$ $= \dfrac{1}{{5\sqrt 2 }} = \dfrac{{\sqrt 2 }}{{10}}$

Chọn C

Câu 19 (TH):

Phương pháp:

Đường tròn tâm $I\left( {a;b} \right)$ và bán kính $R$ có phương trình ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}$

Cách giải:

Bán kính đường tròn là $R = d\left( {I;\Delta } \right)$$= \dfrac{{\left| {4.2 - 3.\left( { - 1} \right) - 1} \right|}}{{\sqrt {{4^2} + {{\left( { - 3} \right)}^2}} }} = 2$

Phương trình đường tròn tâm $I\left( {2; - 1} \right)$ và bán kính $R = 2$ là: ${\left( {x - 2} \right)^2} + {\left( {y + 1} \right)^2} = 4$

Chọn D

Câu 20 (TH):

Phương pháp:

Sử dụng: $\sin \left( {\pi  - \alpha } \right) = \sin \alpha$ , $\cos \left( {\pi  - \alpha } \right) =  - \cos \alpha$

$\sin \left( {\dfrac{\pi }{2} - \alpha } \right) = \cos \alpha ,$ $\tan \left( {\dfrac{\pi }{2} - \alpha } \right) = \cot \alpha$

Cách giải:

Ta có: $\widehat A + \widehat B + \widehat C = \pi$ (tổng ba góc trong tam giác)

+) $\sin \left( {A + B} \right)$ $= \sin \left( {\pi  - C} \right) = \sin C$ nên A sai

+) $\cos \left( {A + B} \right) = \cos \left( {\pi  - C} \right)$ $=  - \cos C$ nên B đúng

+) $\sin \left( {\dfrac{{A + B}}{2}} \right)$ $= \cos \left( {\dfrac{\pi }{2} - \dfrac{{A + B}}{2}} \right) = \cos \dfrac{C}{2}$ nên C đúng

+) $\tan \dfrac{{A + B}}{2}$ $= \cot \left( {\dfrac{\pi }{2} - \dfrac{{A + B}}{2}} \right) = \cot \dfrac{C}{2}$ nên D đúng

Chọn A

Câu 21 (TH):

Phương pháp:

Sử dụng ${\cos ^2}\alpha  = \dfrac{{1 + \cos 2\alpha }}{2}$ và $\sin \left( {a + b} \right) = \sin a\cos b + \cos a\sin b$

Cách giải:

Ta có:

$M = 2{\cos ^2}(\dfrac{\pi }{2} - \dfrac{a}{2}) + \sqrt 2 \sin (\dfrac{\pi }{4} + a) - 1$

$= 2.\dfrac{{1 + \cos \left( {\pi  - a} \right)}}{2}$ $+ \sqrt 2 \left( {\sin a\cos \dfrac{\pi }{4} + \cos a\sin \dfrac{\pi }{4}} \right) - 1$

$= 1 + \cos \left( {\pi  - a} \right)$ $+ \sqrt 2 .\left( {\sin a.\dfrac{1}{{\sqrt 2 }} + \cos a.\dfrac{1}{{\sqrt 2 }}} \right) - 1$

$=  - \cos a + \sin a + \cos a$ $= \sin a$

Chọn A

Câu 22 (TH):

Phương pháp:

Đường thẳng đi qua $M\left( {{x_0};{y_0}} \right)$ và có VTCP $\overrightarrow u  = \left( {a;b} \right)$ có phương trình $\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\end{array} \right.$  

Cách giải:

Gọi đường thẳng cần tìm là $d$

Vì $d \bot \Delta :\left\{ \begin{array}{l}x = 1 - t\\y = 2 + t\end{array} \right.$  nên $d$ nhận $\overrightarrow {{u_\Delta }}  = \left( { - 1;1} \right)$ làm VTPT

Suy ra $\overrightarrow {{u_d}}  = \left( {1;1} \right)$ là 1 VTCP của $d$

Phương trình đường thẳng $d:\left\{ \begin{array}{l}x = t\\y = 2 + t\end{array} \right.$

Chọn D

Câu 23 (VD):

Phương pháp:

Sử dụng: Tam thức $f\left( x \right) = a{x^2} + bx + c < 0$ với $\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta ' < 0\end{array} \right.$  

Cách giải:

Ta có: $f(x) =  - {x^2} + 2(m + 2)x + 9m - 4 < 0$ $\forall x \in \mathbb{R}$

$\Leftrightarrow \left\{ \begin{array}{l}a < 0\\\Delta ' < 0\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l} - 1 < 0\left( {ld} \right)\\{\left( {m + 2} \right)^2} + 9m - 4 < 0\end{array} \right.$ $\Leftrightarrow {m^2} + 13m < 0$ $\Leftrightarrow  - 13 < m < 0$

Mà $m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 12; - 11;...; - 1} \right\}$  nên có 12 giá trị của m thỏa mãn đề bài.

Chọn C

Câu 24 (VD):

Phương pháp:

Sử dụng công thức tính khoảng cách từ $M\left( {{x_0};{y_0}} \right)$ đến đường thẳng $\Delta :ax + by + c = 0$ là:

$d\left( {M;\Delta } \right) = \dfrac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$

Và vẽ hình, lập luận giá trị lớn nhất của khoảng cách.

Cách giải:

Đường tròn $\left( C \right):{\left( {x - 3} \right)^2} + {\left( {y - 3} \right)^2} = 9$ có tâm $I\left( {3;3} \right)$ và bán kính $R = 3.$

Đường thẳng $\Delta :y =  - 2 \Leftrightarrow y + 2 = 0$

Xét $d\left( {I;\Delta } \right) = \dfrac{{\left| {3 + 2} \right|}}{{\sqrt 1 }} = 5 > 3$ nên đường thẳng $\Delta$ không cắt đường tròn $\left( C \right)$

 

Khi đó khoảng cách lớn nhất từ $M \in \left( C \right)$ đến đường thẳng $\Delta$ là $MH$ với $M$ là giao điểm của đường thẳng $d$ đi qua $I$ và vuông góc với $\Delta$ với đường tròn $\left( C \right)$ .

Đường thẳng $d \bot \Delta$ nên có VTCP $\overrightarrow u  = \left( {0;1} \right)$, suy ra $\overrightarrow n  = \left( {1;0} \right)$ là 1 VTPT của $d$

Phương trình đường thẳng $d$: $x - 3 = 0$ $\Leftrightarrow x = 3$

Tọa độ giao điểm của d và $\left( C \right)$ thỏa mãn hệ:

$\left\{ \begin{array}{l}x = 3\\{\left( {x - 3} \right)^2} + {\left( {y - 3} \right)^2} = 9\end{array} \right.$

$\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x = 3\\{\left( {y - 3} \right)^2} = 9\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 3\\y = 0\end{array} \right.\\\left\{ \begin{array}{l}x = 3\\y = 6\end{array} \right.\end{array} \right.\end{array}$

Suy ra ${M_1}\left( {3;0} \right),{M_2}\left( {3;6} \right)$

Ta có $d\left( {{M_1};\Delta } \right) = \dfrac{{\left| 2 \right|}}{1} = 2$ và $d\left( {{M_2};\Delta } \right) = \dfrac{{\left| {6 + 2} \right|}}{1} = 8$

Nên khoảng cách lớn nhất là $8 \Leftrightarrow M \equiv {M_2}\left( {3;6} \right)$

Chọn B

PHẦN TỰ LUẬN

Bài 1 (TH):

Phương pháp:

Tìm điều kiện xác định rồi chuyển vế đổi dấu để giải bất phương trình

Cách giải:

Giải bất phương trình: $x + \sqrt {x - 1}  > \sqrt {x - 1}  - 2$

Điều kiện: $x \ge 1$

Ta có:

$\begin{array}{l}x + \sqrt {x - 1}  > \sqrt {x - 1}  - 2\\ \Leftrightarrow x >  - 2\end{array}$

Kết hợp điều kiện ta có $x \ge 1$

Bất phương trình có tập nghiệm $S = \left[ {1; + \infty } \right)$

Bài 2 (TH):

Phương pháp:

Sử dụng công thức $\cos 2a = 1 - 2{\sin ^2}a$

Cách giải:

Cho $\sin a =  - \dfrac{2}{3}$. Tính $9.\cos 2a$

Ta có: $9.\cos 2a = 9.\left( {1 - 2{{\sin }^2}a} \right)$ $= 9 - 18{\sin ^2}a$ $= 9 - 18.{\left( { - \dfrac{2}{3}} \right)^2}$ $= 1$

Bài 3 (VD):

Phương pháp:

a) Đường thẳng đi qua $M\left( {{x_0};{y_0}} \right)$ và có VTPT $\overrightarrow n  = \left( {a;b} \right)$ có phương trình $a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0$

b) Đường tròn tâm $I\left( {a;b} \right)$ và bán kính $R$ có phương trình ${\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}$

Cách giải:

Cho hai điểm $A(1;2),B(3;4)$.

a) Viết phương trình tổng quát của đường thẳng qua A và vuông góc với AB

Ta có:  $\overrightarrow {AB}  = \left( {2;2} \right)$

Đường thẳng đi qua A và vuông góc với AB nên nhận $\overrightarrow {AB}  = \left( {2;2} \right)$ làm VTPT

Phương trình đường thẳng cần tìm là: $2\left( {x - 1} \right) + 2\left( {y - 2} \right) = 0$ $\Leftrightarrow 2x - 2y - 6 = 0$

$\Leftrightarrow x - y - 3 = 0$

b) Viết phương trình đường tròn đường kính AB

Ta có: $AB = \sqrt {{2^2} + {2^2}}  = 2\sqrt 2$ và trung điểm của $AB$ là $I\left( {\dfrac{{1 + 3}}{2};\dfrac{{2 + 4}}{2}} \right)$ hay $I\left( {2;3} \right)$

Đường tròn có đường kính $AB$ nên có bán kính $R = \dfrac{{AB}}{2} = \sqrt 2$ và có tâm là trung điểm $I\left( {2;3} \right)$ của đoạn $AB.$

Phương trình đường tròn là: ${\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 2$

Bài 4 (VD):

Phương pháp:

Phương trình $a{x^2} + bx + c = 0$ có hai nghiệm phân biệt $\Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\\Delta ' > 0\end{array} \right.$

Cách giải:

Tìm $m$để phương trình  $m{x^2} + 2(m - 1)x - 4 = 0$ có hai nghiệm phân biệt

Phương trình $m{x^2} + 2(m - 1)x - 4 = 0$ có hai nghiệm phân biệt khi:

$\left\{ \begin{array}{l}m \ne 0\\\Delta ' = {\left( {m - 1} \right)^2} + 4m > 0\end{array} \right.$

 $\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\{m^2} - 2m + 1 + 4m > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\{m^2} + 2m + 1 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\{\left( {m + 1} \right)^2} > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne  - 1\end{array} \right.\end{array}$

Vậy với $m \ne 0$ và $m \ne  - 1$ thì phương trình đã cho có hai nghiệm phân biệt

Bài 5 (VDC):

Phương pháp:

Sử dụng định lý hàm số sin cho tam giác $ABC$ : $\dfrac{{AB}}{{\sin C}} = \dfrac{{AC}}{{\sin B}} = \dfrac{{BC}}{{\sin A}} = 2R$

Cách giải:

Chứng minh rằng tam giác ABC vuông  nếu: $\cot \dfrac{B}{2} = \dfrac{{a + c}}{b}$

Áp dụng định lý hàm số sin ta có:$\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}}$$= \dfrac{c}{{\sin C}} = 2R$ với $R$ là bán kính đường tròn ngoại tiếp $\Delta ABC$

$\Leftrightarrow \left\{ \begin{array}{l}a = 2R\sin A\\b = 2R\sin B\\c = 2R\sin C\end{array} \right.$

Khi đó: $\cot \dfrac{B}{2} = \dfrac{{a + c}}{b}$

$\begin{array}{l} \Leftrightarrow \dfrac{{\cos \dfrac{B}{2}}}{{\sin \dfrac{B}{2}}} = \dfrac{{2R\sin A + 2R\sin C}}{{2R\sin B}}\\ \Leftrightarrow \dfrac{{\cos \dfrac{B}{2}}}{{\sin \dfrac{B}{2}}} = \dfrac{{\sin A + \sin C}}{{\sin B}}\\ \Leftrightarrow \dfrac{{\sin B.\cos \dfrac{B}{2}}}{{\sin \dfrac{B}{2}}} = \sin A + \sin C\end{array}$

$\Leftrightarrow \dfrac{{2\sin \dfrac{B}{2}.\cos \dfrac{B}{2}.\cos \dfrac{B}{2}}}{{\sin \dfrac{B}{2}}}$ $= \sin A + \sin C$

$\Leftrightarrow 2{\cos ^2}\dfrac{B}{2} = 2\sin \dfrac{{A + C}}{2}\cos \dfrac{{A - C}}{2}$

$\Leftrightarrow {\cos ^2}\dfrac{B}{2} = \cos \dfrac{B}{2}\cos \dfrac{{A - C}}{2}$ (vì $\dfrac{{A + C}}{2} + \dfrac{B}{2} = \dfrac{\pi }{2}$ nên $\sin \dfrac{{A + C}}{2} = \cos \dfrac{B}{2}$)

$\begin{array}{l} \Leftrightarrow \cos \dfrac{B}{2} = \cos \dfrac{{A - C}}{2}\\ \Rightarrow \dfrac{B}{2} = \dfrac{{A - C}}{2}\\ \Leftrightarrow B = A - C\\ \Leftrightarrow B + C = A\end{array}$

Mà $A + B + C = {180^0}$ (tổng ba góc trong tam giác)

Nên $\widehat A = {90^0}$ hay $\Delta ABC$ vuông tại A.

Loigiaihay.com