Đề kiểm tra 45 phút chương 3 phần Hình học 8 - Đề số 1Đề kiểm tra 45 phút chương 3: Tam giác đồng dạng đề số 1 trang 108 VBT lớp 8 tập 2. Hãy chọn kết quả đúng. Tam giác ABC vuông tại A... Quảng cáo
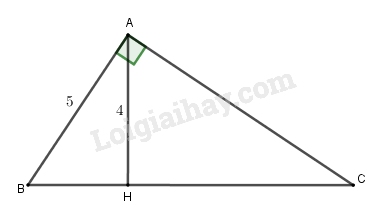
Đề bài Câu 1: Hãy chọn kết quả đúng. Tam giác \(ABC\) vuông tại \(A\) có độ dài \(AB = 5cm\), đường cao \(AH = 4cm\) (h.57).
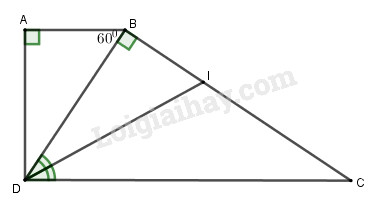
a) Độ dài của \(BH\) là: A. \(3,5\) B. \(4\) C. \(3\) D. \(3,2\) b) Độ dài của \(HC\) là: A. \(\dfrac{8}{3}\) B. \(\dfrac{{20}}{3}\) C. \(\dfrac{{16}}{3}\) D. \(\dfrac{{15}}{4}\) c) Độ dài của \(AC\) là: A. \(\dfrac{{20}}{3}\) B. \(\dfrac{{25}}{3}\) C. \(\dfrac{{25}}{{12}}\) D. \(4\sqrt {\dfrac{5}{6}} \) Câu 2. (7 điểm) Cho hình thang vuông \(ABCD\) \(\left( {AB//CD} \right)\) có \(\widehat A = {90^0}\), cạnh \(BC\) vuông góc với đường chéo \(BD\), đường phân giác của góc \(BDC\) cắt cạnh \(BC\) tại \(I\). Cho biết độ dài \(AB = 2,5cm\) và góc \(\widehat {ABD} = {60^0}\) (h.58) a) Chứng minh rằng \(\Delta IDC\) là tam giác cân. b) Tính độ dài của các cạnh \(BC,AD,DC\) và độ dài của phân giác \(DI\). Lời giải chi tiết Câu 1: Phương pháp: Sử dụng định lý Pi – ta – go trong tam giác vuông và tam giác đồng dạng để tính độ dài các cạnh. Cách giải: a) Tam giác \(AHB\) vuông tại \(H\) nên \(B{H^2} = A{B^2} - A{H^2} = {5^2} - {4^2} = 9\) \( \Rightarrow BH = 3\). Chọn C. b) Xét tam giác \(AHB\) và \(CHA\) có: \(\widehat {AHB} = \widehat {CHA} = {90^0}\left( {gt} \right)\) \(\widehat {HAB} = \widehat {HCA}\) (cùng phụ với góc \(\widehat {CBA}\)) \( \Rightarrow \Delta AHB \backsim \Delta CHA\left( {g.g} \right)\) \( \Rightarrow \dfrac{{AH}}{{CH}} = \dfrac{{HB}}{{HA}}\) \( \Rightarrow HC = \dfrac{{H{A^2}}}{{HB}} = \dfrac{{{4^2}}}{3} = \dfrac{{16}}{3}\) Chọn C. c) Ta có: \(BC = BH + HC = 3 + \dfrac{{16}}{3} = \dfrac{{25}}{3}\) Áp dụng định lí Pi – ta – go cho tam giác vuông \(ABC\) có: \(A{C^2} = B{C^2} - A{B^2}\) \( = {\left( {\dfrac{{25}}{3}} \right)^2} - {5^2} = \dfrac{{400}}{9}\) \( \Rightarrow AC = \dfrac{{20}}{3}\) Chọn A. Câu 2: Phương pháp: a) Chứng minh tam giác \(IDC\) có hai góc \(\widehat {IDC} = \widehat {ICD}\) và suy ra \(IC = ID\). b) Sử dụng các tam giác đồng dạng và định lí Pi – ta – go để tính toán. Chú ý kết quả: Tam giác vuông có một góc bằng \({30^0}\) thì cạnh đối cửa góc bằng nửa cạnh huyền. Cách giải: a) Tam giác \(ABC\) vuông tại \(A\) có: \(\widehat {ABD} + \widehat {ADB} = {90^0}\) (hai góc nhọn trong tam giác vuông) \( \Rightarrow \widehat {ADB} = {90^0} - \widehat {ABD}\) \( = {90^0} - {60^0} = {30^0}\) \( \Rightarrow \widehat {BDC} = \widehat {ADC} - \widehat {ADB}\) \( = {90^0} - {30^0} = {60^0}\) \( \Rightarrow \widehat {IDB} = \widehat {IDC} = \dfrac{{\widehat {BDC}}}{2}\) \( = \dfrac{{{{60}^0}}}{2} = {30^0}\) (1) Tam giác \(BDC\) vuông tại \(B\) có \(\widehat {BDC} + \widehat {BCD} = {90^0}\) (hai góc nhọn trong tam giác vuông) \( \Rightarrow \widehat {BCD} = {90^0} - \widehat {BDC}\) \( = {90^0} - {60^0} = {30^0}\) hay \(\widehat {ICD} = {30^0}\) (2) Từ (1) và (2) suy ra \(\widehat {IDC} = \widehat {ICD}\) nên tam giác \(ICD\) cân tại \(I\) \( \Rightarrow ID = IC\) (đpcm). b) Tam giác \(ABC\) vuông tại \(A\) có \(\widehat {ADB} = {30^0}\) nên \(AB = \dfrac{1}{2}BD\) \( \Rightarrow BD = 2AB = 2.2,5 = 5\left( {cm} \right)\) Áp dụng định lí Pi – ta – go ta có: \(A{D^2} = B{D^2} - A{B^2}\) \( = {5^2} - 2,{5^2} = \dfrac{{75}}{4}\) \( \Rightarrow AD = \sqrt {\dfrac{{75}}{4}} \approx 4,33\left( {cm} \right)\) Tam giác \(BDC\) vuông tại \(B\) có \(\widehat {BCD} = {30^0}\) nên \(BD = \dfrac{1}{2}DC\) \( \Rightarrow DC = 2BD = 2.5 = 10\left( {cm} \right)\) Áp dụng định lí Pi – ta – go ta có: \(B{C^2} = C{D^2} - B{D^2} = {10^2} - {5^2} = 75\) \( \Rightarrow BC = \sqrt {75} \approx 8,66\). Ta có: \(\dfrac{{IB}}{{IC}} = \dfrac{{DB}}{{DC}} = \dfrac{1}{2}\) \( \Rightarrow IC = 2IB\) Mà \(IC + IB = BC = 8,66\) \( \Rightarrow 2IB + IB = 8,66\) \( \Rightarrow 3IB = 8,66 \Rightarrow IB \approx 2,89\) Áp dụng định lí Pi – ta – go ta có: \(D{I^2} = D{B^2} + B{I^2} = {5^2} + 2,{89^2}\) \( \Rightarrow DI = \sqrt {{5^2} + 2,{{89}^2}} \approx 5,78\left( {cm} \right)\). Loigiaihay.com
|




















Danh sách bình luận