Bài 45 trang 104 Vở bài tập toán 8 tập 2

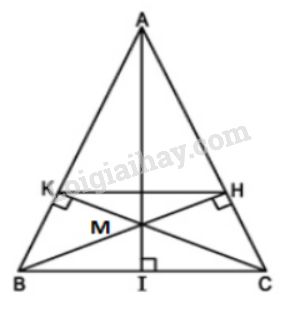
Đề bài

Cho tam giác cân \(ABC (AB = AC)\), vẽ các đường cao \(BH, CK\) (h.53).

a) Chứng minh \(BK = CH\).

b) Chứng minh \(KH//BC\).

c) Cho biết \(BC = a, AB = AC = b\). Tính độ dài đoạn thẳng \(HK\).

Lời giải chi tiết

a) Xét hai tam giác vuông \(BKC\) và \(CHB\), ta có \(\widehat B = \widehat C\) (vì \(AB = AC\))

\(BC\) là cạnh huyền chung.

Suy ra \(\Delta BKC = \Delta CHB \Rightarrow BK = CH\)

b) Từ giả thiết \(AB = AC\) và \(BK = CH\) (theo chứng minh trên) suy ra \(AK = AH\), ta có \(\dfrac{{AK}}{{AB}} = \dfrac{{AH}}{{AC}} \Rightarrow KH//BC\)

c) Vẽ thêm đường cao \(AI\); \(AI,BH,CK\) đồng quy tại \(O\).

\(\Delta IAC \sim \Delta HBC\) (vì \(\widehat I = \widehat H = {90^0}\), góc \(\widehat C\) chung).

Suy ra \(\dfrac{{IC}}{{HC}} = \dfrac{{AC}}{{BC}}\) hay \(\dfrac{{\dfrac{1}{2}a}}{{HC}} = \dfrac{b}{a} \Rightarrow HC = \dfrac{{{a^2}}}{{2b}}\)

\( \Rightarrow AH = b - \dfrac{{{a^2}}}{{2b}} = \dfrac{{2{b^2} - {a^2}}}{{2b}}\)

Từ \(KH//BC\) suy ra \(\dfrac{{AH}}{{AC}} = \dfrac{{KH}}{{BC}}\) \( \Rightarrow KH = \dfrac{{AH.BC}}{{AC}} = \left( {\dfrac{{2{b^2} - {a^2}}}{{2b}}} \right).\dfrac{a}{b}\) \( = a - \dfrac{{{a^3}}}{{2{b^2}}}\)

Loigiaihay.com