Bài 47 trang 106 Vở bài tập toán 8 tập 2

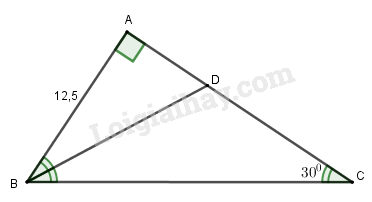
Đề bài

Cho tam giác vuông \(ABC\), và đường phân giác \(BD\) (\(D\) thuộc cạnh \(AC\)).

a) Tính tỉ số \(\dfrac{{A{\rm{D}}}}{{C{\rm{D}}}}\).

b) Cho biết độ dài \(AB = 12,5 cm\). Hãy tính chu vi và diện tích của tam giác \(ABC\).

Lời giải chi tiết

a) Vì \(\widehat A = {90^0}\), \(\widehat C = {30^0}\), suy ra \(AB = \dfrac{1}{2}BC\).

\(BD\) là đường phân giác (h.55), do đó ta có:

\(\dfrac{{DA}}{{DC}} = \dfrac{{AB}}{{BC}} = \dfrac{{\dfrac{1}{2}BC}}{{BC}} = \dfrac{1}{2}.\)

b) \(BC = 2AB = 2.12,5 = 25\left( {cm} \right)\)

\(AC = \sqrt {B{C^2} - A{B^2}} \) \( = \sqrt {{{25}^2} - 12,{5^2}}  \approx 21,65\left( {cm} \right)\)

Gọi \(P\) và \(S\) lần lượt là chu vi và diện tích của tam giác \(ABC\) ta có:

\(P = AB + BC + CA\) \( \approx 12,5 + 25 + 21,65 = 59,15\) \(\left( {cm} \right)\).

\(S = \dfrac{1}{2}AB.AC\) \( \approx \dfrac{1}{2}.12,5.21,65 \approx 135,31\left( {c{m^2}} \right)\)

Loigiaihay.com