Giải bài tập 5.22 trang 65 SGK Toán 12 tập 2 - Cùng khám pháGiả sử một máy bay thương mại M đang bay trên bầu trời theo một đường thẳng từ D đến E có hình chiếu trên mặt đất là đoạn CB. Tại D, máy bay bay cách mặt đất là 9000 m và tại E là 12000 m. Một ra-đa được đặt trên mặt đất tại vị trí O cách C là 20000 m, cách B là 16000 m và (widehat {BOC} = {90^^circ }). Xét hệ trục tọa độ Oxyz (đơn vị: 1000 m) với O là vị trí đặt ra-đa, B thuộc tia Oy, C thuộc tia Ox, khi đó ta có tọa độ các điểm như Hình 5.24. Giả sử ra-đa có bán kính dò tìm tối đa là 1600 Quảng cáo
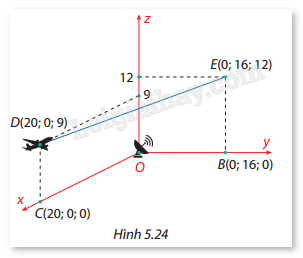
Đề bài Giả sử một máy bay thương mại M đang bay trên bầu trời theo một đường thẳng từ D đến E có hình chiếu trên mặt đất là đoạn CB. Tại D, máy bay bay cách mặt đất là 9000 m và tại E là 12000 m. Một ra-đa được đặt trên mặt đất tại vị trí O cách C là 20000 m, cách B là 16000 m và \(\widehat {BOC} = {90^\circ }\). Xét hệ trục tọa độ Oxyz (đơn vị: 1000 m) với O là vị trí đặt ra-đa, B thuộc tia Oy, C thuộc tia Ox, khi đó ta có tọa độ các điểm như Hình 5.24. Giả sử ra-đa có bán kính dò tìm tối đa là 16000 m. Hỏi ra-đa này có thể dò tìm được tín hiệu của máy bay M khi bay trên bầu trời từ D đến E hay không? Vì sao?
Phương pháp giải - Xem chi tiết - Viết phương trình tham số của đường thẳng DE từ tọa độ điểm \(D\) và \(E\). - Sử dụng công thức khoảng cách từ điểm \(O\) đến đường thẳng DE trong không gian. Nếu khoảng cách nhỏ hơn hoặc bằng bán kính dò tìm \(16000{\mkern 1mu} m\), ra-đa sẽ bắt được tín hiệu máy bay. Lời giải chi tiết Tọa độ điểm \(D(20;0;9)\) và \(E(0;16;12)\). Vectơ chỉ phương của đường thẳng DE là: \(\overrightarrow {DE} = (0 - 20;16 - 0;12 - 9) = ( - 20;16;3)\) Phương trình tham số của đường thẳng DE: \(\left\{ {\begin{array}{*{20}{l}}{x = 20 - 20t}\\{y = 16t}\\{z = 9 + 3t}\end{array}} \right.\) trong đó t là tham số. Gọi H là hình chiếu của O trên đường thẳng DE, suy ra toạ độ điểm M là: \(H(20 - 20t;16t;9 + 3t)\) Và tích vô hướng của \(\overrightarrow {OH} \) và \(\overrightarrow {DE} \) là: \(\overrightarrow {DE} .\overrightarrow {OH} = ( - 20).(20 - 20t) + 16.16t + 3.(9 + 3t) = 0\) Giải phương trình trên ta được điểm \(t = \frac{{373}}{{665}}\) Điểm H có toạ độ là \(\left( {\frac{{1168}}{{133}};\frac{{5968}}{{665}};\frac{{7104}}{{665}}} \right)\) Khoảng cách từ O đến đến đường thẳng DE chính là độ dài đoạn thẳng OH \(d = \sqrt {{{\left( {\frac{{1168}}{{133}}} \right)}^2} + {{\left( {\frac{{5968}}{{665}}} \right)}^2} + {{\left( {\frac{{7104}}{{665}}} \right)}^2}} \approx 16,486 = 16486m\) Vì khoảng cách từ ra-da tới đường bay của máy bay M lớn hơn bán kính dò tìm tối đa của ra-da nên không thể thấy tín hiệu của máy bay M.  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
