Giải bài tập 2.8 trang 65 SGK Toán 12 tập 1 - Cùng khám pháCho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng a và (widehat {BAA'} = widehat {BAD} = widehat {DAA'} = {60^circ }). Tính độ dài đường chéo AC’. Quảng cáo
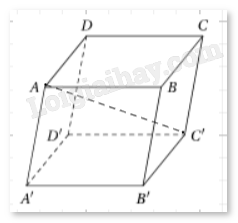
Đề bài Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh đều bằng a và \(\widehat {BAA'} = \widehat {BAD} = \widehat {DAA'} = {60^\circ }\). Tính độ dài đường chéo AC’. Phương pháp giải - Xem chi tiết Sử dụng quy tắc hình hộp và công thức tính tích vô hướng của vectơ, từ đó ta có công thức tính độ dài của \(\overrightarrow {AC'} \) là: \(|\overrightarrow {AC'} | = \sqrt {|\overrightarrow {AB} {|^2} + |\overrightarrow {AD} {|^2} + |\overrightarrow {AA'} {|^2} + 2\overrightarrow {AB} \cdot \overrightarrow {AD} + 2\overrightarrow {AB} \cdot \overrightarrow {AA'} + 2\overrightarrow {AD} \cdot \overrightarrow {AA'} } \) Lời giải chi tiết
Vì tất cả các cạnh đều bằng a và các góc giữa các cặp vectơ đều là \({\rm{\backslash }}({60^\circ }{\rm{ \backslash }})\), ta có: \(|\overrightarrow {AB} | = |\overrightarrow {AD} | = |\overrightarrow {AA'} | = a\) Tích vô hướng giữa các cặp vectơ: \(\overrightarrow {AB} \cdot \overrightarrow {AD} = {a^2}\cos {60^\circ } = \frac{{{a^2}}}{2}\) \(\overrightarrow {AB} \cdot \overrightarrow {AA'} = {a^2}\cos {60^\circ } = \frac{{{a^2}}}{2}\) \(\overrightarrow {AD} \cdot \overrightarrow {AA'} = {a^2}\cos {60^\circ } = \frac{{{a^2}}}{2}\) Vì ABCD.A’B’C’D’ nên: \(\overrightarrow {AC'} = \overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \) Suy ra: \(|\overrightarrow {AC'} | = \sqrt {|\overrightarrow {AB} {|^2} + |\overrightarrow {AD} {|^2} + |\overrightarrow {AA'} {|^2} + 2\overrightarrow {AB} \cdot \overrightarrow {AD} + 2\overrightarrow {AB} \cdot \overrightarrow {AA'} + 2\overrightarrow {AD} \cdot \overrightarrow {AA'} } \) Tính độ dài đường chéo AC': \(|\overrightarrow {AC'} | = \sqrt {{a^2} + {a^2} + {a^2} + 2\left( {\frac{{{a^2}}}{2}} \right) + 2\left( {\frac{{{a^2}}}{2}} \right) + 2\left( {\frac{{{a^2}}}{2}} \right)} \) \(|\overrightarrow {AC'} | = \sqrt {3{a^2} + 3{a^2}} = \sqrt {6{a^2}} = a\sqrt 6 \) Vậy độ dài đường chéo \(AC'\) là \(a\sqrt 6 \).  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
