Giải bài tập 1.9 trang 14 SGK Toán 12 tập 1 - Cùng khám pháCho hàm số \(y = f(x) = 3{x^4} - 16{x^3} + 18{x^2}\) có 1 phần đồ thị như hình 1.10. Tìm giá trị lớn nhất, giá trị nhỏ nhất( nếu có) đã cho trên: a) Nửa khoảng \(( - 1;4]\) b) Đoạn \([ - 1;1]\) Quảng cáo
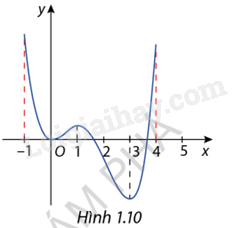
Đề bài Cho hàm số \(y = f(x) = 3{x^4} - 16{x^3} + 18{x^2}\) có 1 phần đồ thị như hình 1.10. Tìm giá trị lớn nhất, giá trị nhỏ nhất( nếu có) đã cho trên: a) Nửa khoảng \(( - 1;4]\) b) Đoạn \([ - 1;1]\)
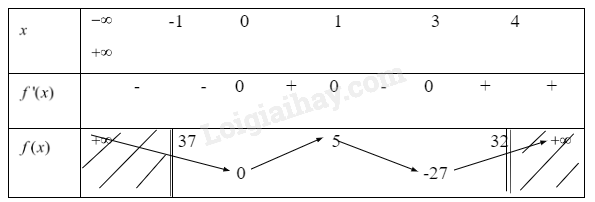
Phương pháp giải - Xem chi tiết Bước 1 Tính \(f'(x)\) Bước 2 Lập bảng biến thiên Bước 3: Tìm cực trị của hàm số trên các đoạn Bước 4 : Suy ra điểm có giá trị lớn nhất, điểm có giá trị bé nhất của hàm số Lời giải chi tiết Ta có: \(f'(x) = 12{x^3} - 48{x^2} + 36x\) Xét \(f'(x) = 0\) \( \Rightarrow 12{x^3} - 48{x^2} + 36x = 0\) \( \Rightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = 3\end{array} \right.\) Từ đó ta có bảng biến thiên là
Từ bảng biến thiên ta thấy a) Hàm số đạt GTLN trên nửa khoảng \(( - 1;4]\) tại x = 4 khi đó y = 32 Hàm số đạt GTNN trên nửa khoảng \(( - 1;4]\) tại x = 3 khi đó y =-27 b) Hàm số đạt GTLN trên đoạn \([ - 1;1]\) tại x = -1 khi đó y = 37 c) Hàm số đạt GTNN trên đoạn \([ - 1;1]\) tại x = 0 khi đó y = 0
|




















Danh sách bình luận