Giải bài tập 13 trang 87 SGK Toán 12 tập 2 - Cánh diềuHình 43 minh hoạ đường bay của một chiếc trực thăng H cất cánh từ một sân bay. Xét hệ trục toạ độ Oxyz có gốc toạ độ O là chân tháp điều khiển của sân bay; trục Ox là hướng đông (Ð), trục Oy là hướng bắc (B) và trục Oz là trục thẳng đứng, đơn vị trên mỗi trục là kilômét. Quảng cáo
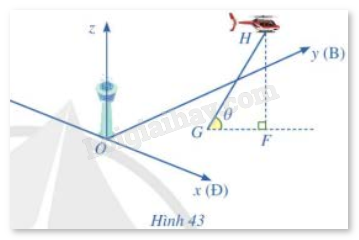
Đề bài Hình 43 minh hoạ đường bay của một chiếc trực thăng H cất cánh từ một sân bay. Xét hệ trục toạ độ Oxyz có gốc toạ độ O là chân tháp điều khiển của sân bay; trục Ox là hướng đông (Ð), trục Oy là hướng bắc (B) và trục Oz là trục thẳng đứng, đơn vị trên mỗi trục là kilômét.
Trực thăng cất cánh từ điểm G. Vectơ \(\overrightarrow r \) chỉ vị trí của trực thăng tại thời điểm t phút sau khi cất cánh (t ≥ 0) có toạ độ là: \(\overrightarrow r = \left( {1 + t;0,5 + 2t;2t} \right)\). a) Tìm góc θ mà đường bay tạo với phương ngang. b) Lập phương trình đường thẳng GF, trong đó F là hình chiếu của điểm H lên mặt phẳng (Oxy). c) Trực thăng bay vào mây ở độ cao 2 km. Tìm toạ độ điểm mà máy bay trực thăng bắt đầu đi vào đám mây. d) Giả sử một đỉnh núi nằm ở điểm M(5; 4,5; 3). Tìm giá trị của t khi HM vuông góc với đường bay GH. Tìm khoảng cách từ máy bay trực thăng đến đỉnh núi tại thời điểm đó. Phương pháp giải - Xem chi tiết a) Sử dụng kiến thức về côsin góc giữa đường thẳng và mặt phẳng để tính: Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( {{a_1};{b_1};{c_1}} \right)\) và mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {{a_2};{b_2};{c_2}} \right)\). Gọi \(\left( {\Delta ,\left( P \right)} \right)\) là góc giữa đường thẳng \(\Delta \) và mặt phẳng (P). Khi đó, \(\sin \left( {\Delta ,\left( P \right)} \right) = \left| {\cos \left( {\overrightarrow u ,\overrightarrow n } \right)} \right| = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\). b) Sử dụng kiến thức về phương trình tham số của đường thẳng để viết phương trình tham số đường thẳng: Hệ phương trình \(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\), trong đó a, b, c không đồng thời bằng 0, t là tham số, được gọi là phương trình tham số của đường thẳng \(\Delta \) đi qua \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {a;b;c} \right)\). c) Trực thăng bay vào mây ở độ cao 2km, tức là vị trí điểm mà trực thăng bắt đầu di chuyển vào đám mây có cao độ \(z = 2\) nên \(2t = 2 \Rightarrow t = 1\). Từ đó tính được tọa độ điểm cần tìm. d) Sử dụng kiến thức về hai đường thẳng vuông góc để tính: HM vuông góc với đường bay GH khi \(\overrightarrow {HM} \bot \overrightarrow {GK} \Leftrightarrow \overrightarrow {HM} .\overrightarrow {GK} = 0\). Lời giải chi tiết a) Góc \(\theta \) là góc giữa đường thẳng GH và mặt phẳng (Oxy). Tại thời điểm \(t = 0\) thì \(\overrightarrow {{r_0}} = \left( {1;0,5;0} \right)\). Trực thăng cất cánh từ điểm G nên G(1; 0,5; 0). Tại thời điểm \(t = 1\), trực thăng bay đến vị trí K thuộc đường thẳng GH với K(2; 2,5; 2). Đường thẳng GH nhận \(\overrightarrow {GK} = \left( {1;2;2} \right)\) làm một vectơ chỉ phương và mặt phẳng (Oxy) nhận \(\overrightarrow k = \left( {0;0;1} \right)\) làm một vectơ pháp tuyến. Ta có: \(\sin \left( {GH,\left( {Oxy} \right)} \right) = \frac{{\left| {1.0 + 2.0 + 2.1} \right|}}{{\sqrt {{1^2} + {2^2} + {2^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{2}{3}\) nên \(\left( {GH,\left( {Oxy} \right)} \right) \approx {42^o}\). Vậy \(\theta \approx {42^o}\). b) Gọi K’ là hình chiếu của K lên mặt phẳng (Oxy). Suy ra, K’(2; 2,5; 0). Vì F là hình chiếu của H lên mặt phẳng (Oxy) nên \(K' \in GF\). Suy ra, đường thẳng GF có một vectơ chỉ phương là \(\overrightarrow {GK'} = \left( {1;2;0} \right)\). Phương trình tham số của đường thẳng GF: \(\left\{ \begin{array}{l}x = 1 + t'\\y = 0,5 + 2t'\\z = 0\end{array} \right.\) (\(t'\) là tham số). c) Trực thăng bay vào mây ở độ cao 2km, tức là vị trí điểm mà trực thăng bắt đầu di chuyển vào đám mây có cao độ \(z = 2\) nên \(2t = 2 \Rightarrow t = 1\). Vậy tọa độ điểm mà trực thăng bắt đầu đi vào đám mây là (2; 2,5; 2). d) Ta có: \(H\left( {1 + t;0,5 + 2t;2t} \right)\), \(\overrightarrow {HM} = \left( {4 - t;4 - 2t;3 - 2t} \right)\). HM vuông góc với đường bay GH khi \(\overrightarrow {HM} \bot \overrightarrow {GK} \Leftrightarrow \overrightarrow {HM} .\overrightarrow {GK} = 0\) \( \Leftrightarrow \left( {4 - t} \right).1 + \left( {4 - 2t} \right).2 + \left( {3 - 2t} \right).2 = 0 \Leftrightarrow t = 2\) Vậy \(t = 2\) thì HM vuông góc với đường bay GH. Khi đó, khoảng cách từ máy bay trực thăng đến đỉnh núi là: \(HM = \sqrt {{{\left( {4 - 2} \right)}^2} + {{\left( {4 - 2.2} \right)}^2} + {{\left( {3 - 2.2} \right)}^2}} = \sqrt 5 \left( {km} \right)\)
|




















Danh sách bình luận