Giải bài tập 1.24 trang 35 SGK Toán 12 tập 1 - Cùng khám pháMột chất điểm chuyển động theo quy luật \(s(t) = - {t^3} + 2t - t\), với 𝑡 (đơn vị: giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và 𝑠 (đơn vị: mét) là quãng đường chất điểm di chuyển được trong khoảng thời gian đó. a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số 𝑠=𝑠(𝑡) trên hệ trục tọa độ 𝑡0𝑠. b) Trong khoảng thời gian 2 giây kể từ khi bắt đầu chuyển động, chất điểm đạt được vận tốc lớn nhất là bao nhiêu? Quảng cáo
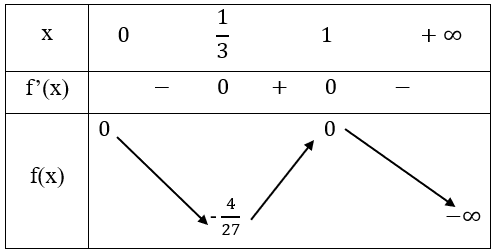
Đề bài Một chất điểm chuyển động theo quy luật \(s(t) = - {t^3} + 2t - t\), với 𝑡 (đơn vị: giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và 𝑠 (đơn vị: mét) là quãng đường chất điểm di chuyển được trong khoảng thời gian đó. a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số 𝑠=𝑠(𝑡) trên hệ trục tọa độ 𝑡0𝑠. b) Trong khoảng thời gian 2 giây kể từ khi bắt đầu chuyển động, chất điểm đạt được vận tốc lớn nhất là bao nhiêu? Phương pháp giải - Xem chi tiết a) - Tìm tập xác định của hàm số - Xét sự biến thiên của hàm số - Vẽ đồ thị hàm số b) - Xác định biểu thức vận tốc. - Tìm các điểm t trong khoảng từ 0 đến 2 để v(t) đạt cực trị. Lời giải chi tiết a) - Tập xác định: \(D = \{ x \ge 0,x \in R\} \) - Tính đạo hàm: \(s'(t) = - 3{t^2} + 4t - 1\) Giải phương trình: \(s'(t) = 0 \Leftrightarrow - 3{t^2} + 4t - 1 = 0 \Rightarrow {t_1} = 1,{t_2} = \frac{1}{3}\) - Giới hạn \(\mathop {\lim }\limits_{t \to \infty } s(t) = \mathop {\lim }\limits_{t \to \infty } \left( { - {t^3} + 2{t^2} - t} \right) = - \infty \) - Bảng biến thiên:
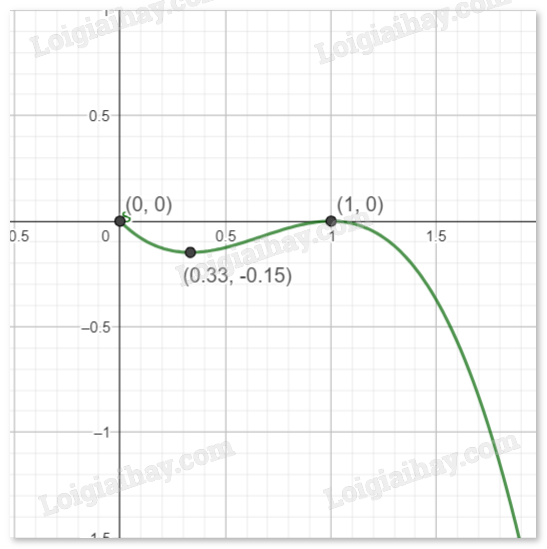
- Vẽ đồ thị Hàm số nghịch biến trên khoảng (0, \(\frac{1}{3}\)) và (1,∞) Hàm số đồng biến trên khoảng (\(\frac{1}{3}\),1) Cực trị: Hàm số đạt cực tiểu tại \(x = \frac{1}{2},{y_{CT}} = - \frac{4}{{27}}\) Hàm số đạt cực đại tại \(x = 1,{y_{CD}} = 0\)
b) Ta có vận tốc: \(v(t) = s'(t) = - 3{t^2} + 4t - 1\) Điểm cực trị của vận tốc: Giải \(s''(t) = 0\): \( - 6t + 4 = 0 \Rightarrow t = \frac{2}{3}\) Vận tốc tại các điểm biên và cực trị: \(\begin{array}{l}v(0) = - {3.0^2} + 4.0 - 1 = - 1\\v\left( {\frac{2}{3}} \right) = - 3{\left( {\frac{2}{3}} \right)^2} + 4\left( {\frac{2}{3}} \right) - 1 = - \frac{{12}}{9} + \frac{8}{3} - 1 = - \frac{4}{3} + \frac{8}{3} - 1 = \frac{1}{3}\\v(2) = - 3 \cdot {2^2} + 4 \cdot 2 - 1 = - 12 + 8 - 1 = - 5\end{array}\) Vậy, vận tốc lớn nhất trong khoảng thời gian 2 giây là \(\frac{1}{3}\) m/s.  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
