Giải bài tập 10 trang 47 SGK Toán 12 tập 1 - Cánh diềuMột trang sách có dạng hình chữ nhật với diện tích là 384 cm². Sau khi để lề trên và lề dưới đều là 3 cm, để lề trái và lề phải đều là 2 cm. Phần còn lại của trang sách được in chữ. Kích thước tối ưu của trang sách là bao nhiêu để phần in chữ trên trang sách có diện tích lớn nhất? Quảng cáo
Đề bài
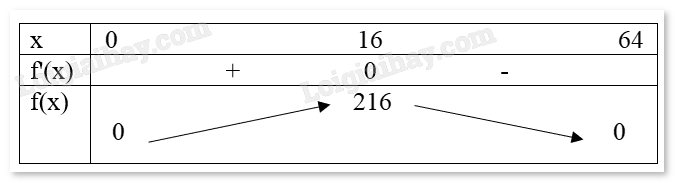
Một trang sách có dạng hình chữ nhật với diện tích là 384 cm². Sau khi để lề trên và lề dưới đều là 3 cm, để lề trái và lề phải đều là 2 cm. Phần còn lại của trang sách được in chữ. Kích thước tối ưu của trang sách là bao nhiêu để phần in chữ trên trang sách có diện tích lớn nhất? Phương pháp giải - Xem chi tiết Phân tích đề bài. Tìm các mối quan hệ trong bài. Lập phương trình và giải. Lời giải chi tiết Giả sử chiều rộng của trang sách là x và chiều dài là y. Theo đề bài, diện tích của trang sách là: $xy~=~384~cm{}^\text{2}$. Khi để lề trên và lề dưới đều là 3 cm, lề trái và lề phải đều là 2 cm thì diện tích phần in chữ sẽ là: \(\left( {y - 2.3} \right)\left( {x - 2.2} \right)\; = \;\left( {y - 6} \right)\left( {x - 4} \right)\) Ta có: \(x = \frac{{384}}{y}\). Thay x vào phương trình \(\left( {y - 6} \right)\left( {x - 4} \right)\) ta thu được \(\left( {x - 4} \right)\left( {\frac{{384}}{x} - 6} \right)\). Xét \(f\left( x \right) = \;\left( {x - 4} \right)\left( {\frac{{384}}{x} - 6} \right)\) \( = \frac{{ - 6{x^2} + 408x - 1536}}{x}\) với \(x \in (4;64)\) do \(\left\{ {\begin{array}{*{20}{c}}{x - 4 > 0}\\{\frac{{384}}{x} - 6 > 0}\end{array}} \right.\). Ta có: \(f'(x) = \frac{{ - 6{x^2} + 1536}}{{{x^2}}} = 0 \Leftrightarrow x = \pm 16\). Với \(x \in (4;64)\) thì chỉ xét x = 16. Ta có bảng biến thiên:
Với \(x = 16\) thì \(y = \frac{{384}}{x} = \frac{{384}}{{16}} = 24\). Vậy kích thước của trang sách có chiều dài 24 cm, chiều rộng 16 cm thì phần in chữ trên trang sách có diện tích lớn nhất.  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
