Giải bài 9.3 trang 82 SGK Toán 8 tập 2 - Kết nối tri thức

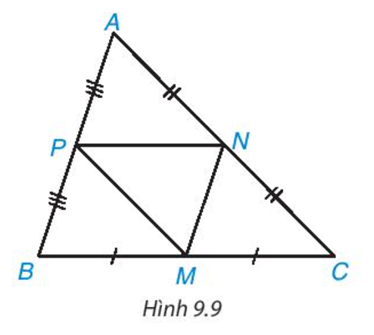
Đề bài

Trong hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng 

 

Lời giải chi tiết

- Có AP = BP, NA = NC

=> NP // BC (P ∈ AB, N ∈ AC)

=> ΔABC \(\backsim\) ΔAPN 

- Có AP = BP, MB = MC

=> MP // AC (P ∈ AB, M ∈ BC)

=> ΔABC \(\backsim\) ΔPBM
- Có NA = NC, MB = MC

=> MN // AB (N ∈ AC,M ∈ BC)

=> ΔABC \(\backsim\) ΔNMC

- Có ΔABC \(\backsim\) ΔAPN và ΔABC \(\backsim\) ΔPBM => ΔAPN \(\backsim\) ΔPBM

- Có ΔABC \(\backsim\) ΔNMC và ΔABC \(\backsim\) ΔPBM => ΔNMC \(\backsim\) ΔPBM 

- Có ΔAPN \(\backsim\) ΔPBM và ΔNMC \(\backsim\) ΔPBM => ΔAPN \(\backsim\) ΔNMC