Giải bài 9.27 trang 103 SGK Toán 8 tập 2 - Kết nối tri thức

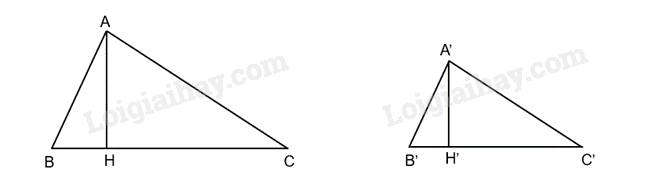
Đề bài

Cho tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k. Gọi A'H' và AH lần lượt là các đường cao đỉnh A' và A của tam giác A'B'C' và tam giác ABC. Chứng minh rằng:

a) \(\frac{{A'H'}}{{AH}} = k\)

b) Diện tích tam giác A'B'C' bằng \(k^2\) lần diện tích tam giác ABC

Lời giải chi tiết

a) Vì ΔA′B′C′ ∽ ΔABC 

=> \(\widehat B = \widehat {B'};\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\)

Xét hai tam giác vuông A'H'B' (vuông tại H') và tam giác vuông AHB (vuông tại H), có: 

\(\widehat B = \widehat {B'}\)

=> ΔA′H′B′ ∽ ΔAHB 

=> \(\frac{{A'H'}}{{AH}} = \frac{{A'B'}}{{AB}}\)

Mà \(\frac{{A'B'}}{{AB}} = k\)

=> \(\frac{{A'H'}}{{AH}} = k\)

b) Có diện tích tam giác ABC là: \(\frac{1}{2}\)AH.BC

   Có diện tích tam giác A'B'C' là: \(\frac{1}{2}\)A′H′.B′C′

Xét tỉ lệ giữa hai tam giác A'B'C' và tam giác ABC có:

\(\frac{{\frac{1}{2}A'H'.B'C'}}{{\frac{1}{2}AH.BC}} = \frac{{A'H'}}{{AH}}.\frac{{B'C'}}{{BC}} = k.k = {k^2}\)