Giải Bài 9.21 trang 58 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

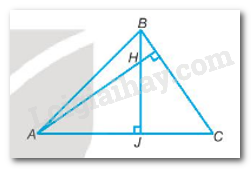
Đề bài

Gọi H là trực tâm của tam giác nhọn ABC. Khi AH = BC, hãy chứng minh \(\widehat {BAC} = {45^0}\).

Lời giải chi tiết

Gọi BJ là đường cao xuất phát từ B của tam giác ABC

\( \Rightarrow BJ \bot AC\)

Xét \(\Delta AHJ\) và \(\Delta BCJ\) có:

\(\begin{array}{l}\widehat {AJH} = \widehat {BJC} = {90^0}\\\left\{ \begin{array}{l}\widehat {JAH} + \widehat {JCB} = {90^0}\\\widehat {JBC} + \widehat {JCB} = {90^0}\end{array} \right. \Rightarrow \widehat {JAH} = \widehat {JBC}\\AH = BC\left( {gt} \right)\\ \Rightarrow \Delta AHJ = \Delta BCJ\left( {ch - gn} \right)\end{array}\)

\( \Rightarrow AJ = BJ\)(cạnh tương ứng)

Mà tam giác JAB vuông tại J nên JAB là tam giác vuông cân.

Vậy \(\widehat {BAC} = {45^0}\)