Giải Bài 71 trang 89 sách bài tập toán 7 - Cánh diều

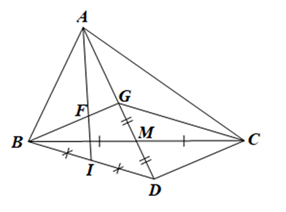
Đề bài

 Cho tam giác ABC có trọng tâm G. Gọi M là trung điểm của BC. Trên tia đối của MG lấy điểm D sao cho MD = MG.

a) Chứng minh CG là trung tuyến của tam giác ACD.

b) Chứng minh BG song song với CD.

c) Gọi I là trung điểm của BD; AI cắt BG tại F. Chứng minh AF = 2FI.

Lời giải chi tiết

 

a) Vì G là trọng tâm tam giác ABC nên \(GM = \frac{1}{2}GA\).

Mà MD = MG (giả thiết) nên M là trung điểm của GD và \(GM = \frac{1}{2}G{\rm{D}}\)

Suy ra GD = GA.

Do đó CG là trung tuyến của tam giác ACD.

Vậy CG là trung tuyến của tam giác ACD.

b) Xét ∆BGM và ∆CDM có:

GM = DM (giả thiết),

\(\widehat {GMB} = \widehat {DMC}\) (hai góc đối đỉnh),

MB = MC (vì M là trung điểm của BC)

Nên ∆BGM = ∆CDM (c.g.c).

Suy ra \(\widehat {BGM} = \widehat {CDM}\) (hai góc tương ứng).

Mà chúng ở vị trí so le trong nên BG // CD.

Vậy BG // CD.

c) Trong tam giác ABD có AI và BG là hai đường trung tuyến, AI và BG cắt nhau tại F.

Do đó F là trọng tâm của tam giác ABD.

Suy ra FI = 1212FA hay AF = 2FI.

Vậy AF = 2FI.