Giải Bài 73 trang 90 sách bài tập toán 7 - Cánh diều

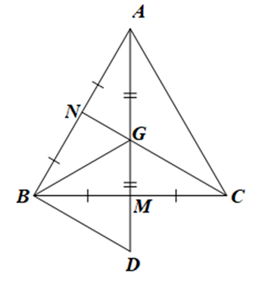
Đề bài

Cho tam giác ABC đều và có G là trọng tâm.

a) Chứng minh GA = GB = GC.

b) Trên tia AG lấy điểm D sao cho GD = GA. Chứng minh tam giác BGD là tam giác đều.

Lời giải chi tiết

 

a) • Do tam giác ABC đều nên AB = BC = AC.

Gọi M, N lần lượt là trung điểm của BC và AB.

Khi đó \(AN = NB = \frac{1}{2}AB = \frac{1}{2}BC = BM = MC\)

Xét ∆ABM và ∆CBN có:

AB = BC (giả thiết),

\(\widehat {ABC}\) là góc chung,

BM = BN (chứng minh trên)

Do đó ∆ABM = ∆CBN (c.c.c).

Suy ra AM = CN (hai cạnh tương ứng).

• Vì G là trọng tâm tam giác ABC

Nên \(AG = \frac{2}{3}AM\) và \(CG = \frac{2}{3}CN\) (tính chất trọng tâm của tam giác).

Mà AM = CN.

Suy ra GA = GC.

Chứng minh tương tự ta có GA = GB.

Do đó GA = GB = GC.

Vậy GA = GB = GC.

b) Ta có GA = GB (theo câu a) và GA = GD (giả thiết).

Nên GD = GB (1)

Ta có G là trọng tam giác ABC nên \(GM = \frac{1}{2}GA\)

Mà GA = GD nên \(GM = \frac{1}{2}G{\rm{D}}\).

Do đó\(GM = M{\rm{D}} = \frac{1}{2}G{\rm{D}}\).

Xét ∆GMC và ∆DMB có:

MB = MC (chứng minh câu a),

\(\widehat {GMC} = \widehat {DMB}\) (hai góc đối đỉnh),

MG = MD (chứng minh trên).

Do đó ∆GMC = ∆DMB (c.g.c)

Suy ra GC = DB (hai cạnh tương ứng).

Lại có GC = GB (theo câu a)

Nên GB = DB (2)

Từ (1) và (2) suy ra GD = GB = DB.

Do đó tam giác BGD là tam giác đều.

Vậy tam giác BGD là tam giác đều