Giải bài 5.21 trang 65 sách bài tập toán 9 - Kết nối tri thức tập 1Cho tam giác ABC vuông tại A, có đường cao AH. a) Chứng minh rằng BC tiếp xúc với đường tròn (A) bán kính AH; b) Gọi M và N là các điểm đối xứng với H lần lượt qua AB và AC. Chứng minh rằng BM và CN là hai tiếp tuyến của (A); c) Chứng minh rằng MN là một đường kính của (A); d) Tính diện tích của tứ giác BMNC, biết (HB = 2cm) và (HC = 4,5cm). Quảng cáo
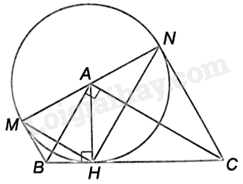
Đề bài Cho tam giác ABC vuông tại A, có đường cao AH. a) Chứng minh rằng BC tiếp xúc với đường tròn (A) bán kính AH; b) Gọi M và N là các điểm đối xứng với H lần lượt qua AB và AC. Chứng minh rằng BM và CN là hai tiếp tuyến của (A); c) Chứng minh rằng MN là một đường kính của (A); d) Tính diện tích của tứ giác BMNC, biết \(HB = 2cm\) và \(HC = 4,5cm\). Phương pháp giải - Xem chi tiết a) + Chỉ ra \(AH \bot BC\) tại H, H thuộc (A, AH) nên BC tiếp xúc với đường tròn (A) bán kính AH. b) + Chứng minh \(\Delta AMB = \Delta AHB\left( {c.c.c} \right)\). Do đó, \(\widehat {AMB} = \widehat {AHB} = {90^o}\). + Chứng minh M thuộc đường tròn (A). Suy ra, BM vuông góc với AM tại M nên BM là tiếp tuyến của (A) tại M. + Chứng minh \(\Delta ANC = \Delta AHC\left( {c.c.c} \right)\). Do đó, \(\widehat {ANC} = \widehat {AHC} = {90^o}\). + Chỉ ra N thuộc đường tròn (A). + Suy ra, CN vuông góc với AN tại N nên AN là tiếp tuyến của (A) tại N. c) + Chứng minh \(\widehat {MAB} = \widehat {HAB}\), \(\widehat {NAC} = \widehat {HAC}\), \(\widehat {HAB} + \widehat {HAC} = {90^o}\). + Do đó, \(\widehat {MAB} + \widehat {HAB} + \widehat {NAC} + \widehat {HAC} = {180^o}\) + Suy ra, ba điểm M, A, N thẳng hàng. Vậy MN là đường kính của (A). d) + Chứng minh \(BM = BH\), \(CN = CH\). + Do đó, \(BM + CN = BH + CH = 2 + 4,5 = 6,5\left( {cm} \right)\) + Chứng minh $\Delta HBA\backsim \Delta HAC\left( g.g \right)$ nên \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\), từ đó tính được AH, tính được MN. + Chứng minh tứ giác BMNC là hình thang vuông. + Diện tích hình thang BMNC là: \(S = \frac{1}{2}MN\left( {BM + CN} \right)\). Lời giải chi tiết
a) Vì AH là đường cao của tam giác ABC nên \(AH \bot BC\) tại H. Mà H thuộc (A, AH) nên BC tiếp xúc với đường tròn (A) bán kính AH. b) Vì M đối xứng với H qua AB nên \(AM = AH\) và \(BM = BH\), AB chung nên \(\Delta AMB = \Delta AHB\left( {c.c.c} \right)\). Do đó, \(\widehat {AMB} = \widehat {AHB} = {90^o}\). Lại có \(AM = AH\) nên M thuộc đường tròn (A). Suy ra, BM vuông góc với AM tại M nên BM là tiếp tuyến của (A) tại M. Vì N đối xứng với H qua AC nên \(CN = CH\) và \(AH = AN\), AC chung nên \(\Delta ANC = \Delta AHC\left( {c.c.c} \right)\). Do đó, \(\widehat {ANC} = \widehat {AHC} = {90^o}\). Lại có \(AH = AN\) nên N thuộc đường tròn (A). Suy ra, CN vuông góc với AN tại N nên AN là tiếp tuyến của (A) tại N. c) Vì \(\Delta AMB = \Delta AHB\left( {cmt} \right)\) nên \(\widehat {MAB} = \widehat {HAB}\). Vì \(\Delta ANC = \Delta AHC\left( {cmt} \right)\) nên \(\widehat {NAC} = \widehat {HAC}\). Vì \(AH \bot BC\) tại H nên \(\widehat {HAB} + \widehat {HAC} = {90^o}\). Do đó, \(\widehat {MAB} + \widehat {HAB} + \widehat {NAC} + \widehat {HAC} \) \(= 2\left( {\widehat {HAB} + \widehat {HAC}} \right) \) \(= {2.90^o} = {180^o}\) Suy ra, ba điểm M, A, N thẳng hàng. Mà \(AM = AN\left( { = AH} \right)\) nên MN là đường kính của (A). d) Vì MB và BH là hai tiếp tuyến cắt nhau tại B của (A) nên \(BM = BH\). Vì CN và CH là hai tiếp tuyến cắt nhau tại C của (A) nên \(CN = CH\). Do đó, \(BM + CN = BH + CH = 2 + 4,5 = 6,5\left( {cm} \right)\). Ta có: \(\widehat {BAH} + \widehat {ABC} = \widehat {ACH} + \widehat {ABC}\\\left( { = {{90}^o}} \right)\) nên \(\widehat {BAH} = \widehat {ACH}\). Mà \(\widehat {BHA} = \widehat {CHA} = {90^o}\) nên $\Delta HBA\backsim \Delta HAC\left( g.g \right)$ nên \(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\), suy ra \(A{H^2} = BH.CH = 4,5.2 = 9\). Suy ra \(AH = 3cm\). Do đó, \(MN = 2AH = 6cm\). Ta có: \(BM \bot MN,CN \bot MN\) nên BM//NC. Do đó, tứ giác BMNC là hình thang vuông. Diện tích hình thang BMNC là: \(S = \frac{1}{2}MN\left( {BM + CN} \right) = \frac{1}{2}.6.6,5 = 19,5\left( {c{m^2}} \right)\).
|




















Danh sách bình luận