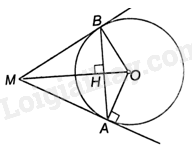
Giải bài 5.19 trang 65 sách bài tập toán 9 - Kết nối tri thức tập 1

Đề bài

Cho đường tròn (O) và điểm M nằm bên ngoài (O). Từ M kẻ tiếp tuyến MA với (O), trong đó A là tiếp điểm. Đường thẳng qua A và vuông góc với MO cắt (O) tại B (khác A).

a) Chứng minh rằng MB là tiếp tuyến của (O);

b) Tính OM và diện tích phần của tam giác AMB nằm bên ngoài (O), biết bán kính của (O) bằng 3cm và \(\widehat {MAB} = {60^o}\).

Lời giải chi tiết

a) Gọi H là giao điểm của MO và AB. Do đó, MO vuông góc với AB tại H.

Tam giác AOH và tam giác BOH có:

OH chung, \(OA = OB\), \(\widehat {OHA} = \widehat {BHO} = {90^o}\)

nên \(\Delta AOH = \Delta BOH\left( {ch - cgv} \right)\)

nên \(\widehat {AOH} = \widehat {BOH}\) hay \(\widehat {AOM} = \widehat {BOM}\).

Tam giác AOM và tam giác BOM có:

OM chung, \(OA = OB\), \(\widehat {AOM} = \widehat {BOM}\)

nên \(\Delta AOM = \Delta BOM\left( {c - g - c} \right)\)

nên \(\widehat {MAO} = \widehat {MBO} = {90^o}\) .

Do đó, \(MB \bot OB\) tại B.

Do đó, MB là tiếp tuyến của (O).

b) Vì MA và MB là hai tiếp tuyến của (O) nên \(MA = MB\).

Do đó, tam giác MAB cân tại M.

Mà \(\widehat {MAB} = {60^o}\) nên tam giác MAB đều.

Do đó, \(\widehat {AMB} = {60^o}\).

Tứ giác AOBM có:

\(\widehat {AOB} + \widehat {OBM} + \widehat {BMA} + \widehat {MAO} = {360^o}\)

Suy ra:

\(\widehat {AOB} = {360^o} - \left( {\widehat {OBM} + \widehat {BMA} + \widehat {MAO}} \right) \\= {360^o} - \left( {{{90}^o} + {{90}^o} + {{60}^o}} \right) = {120^o}\)

Vì AOB là góc ở tâm chắn cung nhỏ AB nên sđ$\overset\frown{AB}$_nhỏ \( = {120^o}\).

Do đó, diện tích hình quạt tròn ứng với cung nhỏ AB là:

\({S_q} = \frac{{120}}{{360}}.\pi {.3^2} = 3\pi \left( {c{m^2}} \right)\)

Vì MA và MB là hai tiếp tuyến của (O) nên OM là phân giác của góc AOB nên \(\widehat {AOM} = \frac{1}{2}\widehat {AOB} = {60^o}\).

Tam giác MOA vuông tại A nên

\(AM = AO.\tan \widehat {AOM} = 3.\tan {60^o} = 3\sqrt 3 \left( {cm} \right)\).

Vì \(\Delta AOM = \Delta BOM\left( {cmt} \right)\)

nên \({S_{\Delta AMO}} = {S_{\Delta BMO}} \) \(= \frac{1}{2}OA.AM = \frac{1}{2}.3.3\sqrt 3  \) \( = \frac{{9\sqrt 3 }}{2}\left( {c{m^2}} \right)\).

Do đó diện tích tứ giác AOBM là:

\({S_{AOBM}} = 2{S_{\Delta AMO}} = 9\sqrt 3 \left( {c{m^2}} \right)\).

Vậy diện tích phần của tam giác AMB nằm bên ngoài (O) là:

\(S = {S_{AOBM}} - {S_q} = 9\sqrt 3  - 3\pi \left( {c{m^2}} \right)\).