Giải bài 5.20 trang 65 sách bài tập toán 9 - Kết nối tri thức tập 1Cho AM và AN là hai tiếp tuyến cắt nhau của đường tròn (O), trong đó M và N là hai tiếp điểm. Gọi E là một điểm thuộc cung nhỏ MN. Tiếp tuyến của (O) tại E cắt AM tại B và cắt AN tại C. Biết (AB = 10cm), (AC = 7cm) và (BC = 6cm). Tính độ dài của các đoạn thẳng AM, AN, BM và CN. Quảng cáo
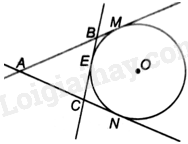
Đề bài Cho AM và AN là hai tiếp tuyến cắt nhau của đường tròn (O), trong đó M và N là hai tiếp điểm. Gọi E là một điểm thuộc cung nhỏ MN. Tiếp tuyến của (O) tại E cắt AM tại B và cắt AN tại C. Biết \(AB = 10cm\), \(AC = 7cm\) và \(BC = 6cm\). Tính độ dài của các đoạn thẳng AM, AN, BM và CN. Phương pháp giải - Xem chi tiết + Dựa vào tính chất hai tiếp tuyến cắt nhau ta có \(AM = AN\), \(BM = BE\), \(CE = CN\). + \(AM + AN = AB + AC + CE\), từ đó tính được AM, AN. + \(BM = AM - AN,CN = AN - CN\). Lời giải chi tiết
Vì AM và AN là hai tiếp tuyến cắt nhau của (O) nên \(AM = AN\). Vì BM và BE là hai tiếp tuyến cắt nhau của (O) nên \(BM = BE\). Vì CE và CN là hai tiếp tuyến cắt nhau của (O) nên \(CE = CN\). Ta có: \(AM + AN = AB + BM + AC + CN \) \(= AB + BE + AC + CE = AB + AC + \left( {BE + CE} \right)\) \( = AB + AC + BC\) Suy ra \(2AM = 10 + 7 + 6 = 23\left( {cm} \right)\) nên \(AM = AN = 11,5\left( {cm} \right)\) \(BM = AM - AB = 11,5 - 10 = 1,5\left( {cm} \right),\) \(CN = AN - AC = 11,5 - 7 = 4,5\left( {cm} \right)\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
