Giải Bài 51 trang 84 sách bài tập toán 7 - Cánh diều

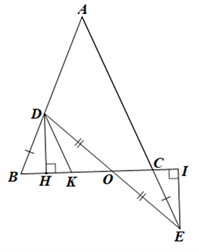
Đề bài

Cho tam giác ABC. Trên cạnh BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho CE = BD. Gọi O là giao điểm của DE và BC. Biết OD = OE. Chứng minh tam giác ABC là tam giác cân.

Lời giải chi tiết

 

Qua D vẽ DK // AC (K ∈ BC) nên \(\widehat {KDO} = \widehat {OEC}\) (hai góc so le trong).

Xét DOKD và DOCE có:

\(\widehat {KDO} = \widehat {OEC}\) (chứng minh trên),

OD = OE (giả thiết),

\(\widehat {DOK} = \widehat {EOC}\) (hai góc đối đỉnh).

Do đó ∆OKD = ∆OCE (g.c.g).

Suy ra KD = CE (hai cạnh tương ứng).

Mặt khác BD = CE suy ra DB = DK hay tam giác DBK cân tại D.

Suy ra \(\widehat {DBK} = \widehat {DKB}\) (1)

Do DK // AC nên \(\widehat {DKB} = \widehat {ACB}\) (hai góc đồng vị) (2)

Từ (1) và (2) ta có: \(\widehat {ABC} = \widehat {ACB}\)

Suy ra tam giác ABC cân tại A.

Vậy tam giác ABC là tam giác cân tại A.