Giải bài 4.9 trang 83 SGK Toán 8 tập 1 - Kết nối tri thứcCho hình chữ nhật ABCD có AC cắt BD tại O. Quảng cáo
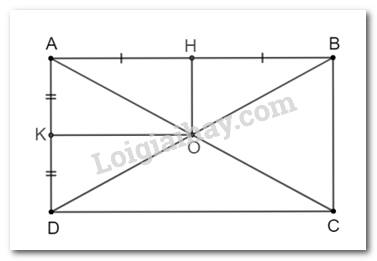
Đề bài Cho hình chữ nhật ABCD có AC cắt BD tại O. Gọi H, K lần lượt là trung điểm của AB, AD. Chứng minh tứ giác AHOK là hình chữ nhật. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Chứng minh tứ giác AHOK có 3 góc vuông nên là hình chữ nhật. Lời giải chi tiết
Vì ABCD là hình chữ nhật nên \(\widehat {BA{\rm{D}}} = {90^o}\) và hai đường chéo AC, BD bằng nhau và cắt nhau tại trung điểm O của mỗi đường. Suy ra AB ⊥ AD; O là trung điểm của AC và BD. Vì O, H lần lượt là trung điểm của BD và AB nên OH là đường trung bình của tam giác ABD. Suy ra OH // AD mà AB ⊥ AD nên OH ⊥ AB hay \(\widehat {AHO} = {90^o}\) Tương tự, ta chứng minh được: OK ⊥ AD hay \(\widehat {AK{\rm{O}}} = {90^o}\). Ta có: \(\widehat {BA{\rm{D}}} + \widehat {AHO} + \widehat {AK{\rm{O}}} + \widehat {HOK} = {360^o}\) 90°+90°+90°+\(\widehat {HOK}\)=360° 270°+\(\widehat {HOK}\)=360° Suy ra \(\widehat {HOK}\)=360°−270°=90° Tứ giác AHOK có \(\widehat {BA{\rm{D}}}\)=90°;ˆAHO=90°; \(\widehat {AHO}\)=90°;\(\widehat {AK{\rm{O}}}\)=90o Do đó, tứ giác AHOK là hình chữ nhật.
|




















Danh sách bình luận