Giải bài 4.7 trang 50 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Đề bài

Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương. Chứng minh rằng

\(\left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| < \left| {\overrightarrow a  + \overrightarrow b } \right| < \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\)

Lời giải chi tiết

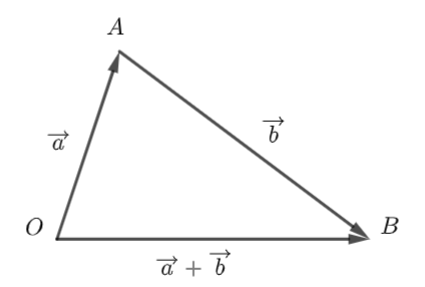
Gọi điểm \(O\) bất kỳ, vẽ vectơ \(\overrightarrow {OA}  = \overrightarrow a ,\,\,\overrightarrow {AB}  = \overrightarrow b \)

\( \Rightarrow \) \(\overrightarrow {OB}  = \overrightarrow {OA}  + \overrightarrow {AB}  = \overrightarrow a  + \overrightarrow b \)

Vì hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương nên \(O,\,\,A,\,\,B\) không thẳng hàng.

Xét \(\Delta ABC,\) áp dụng bất đẳng thức tam giác ta có:

\(\begin{array}{l}OA - AB < OB < OA + AB\\ \Leftrightarrow \left| {\overrightarrow a } \right| - \left| {\overrightarrow b } \right| < \left| {\overrightarrow a  + \overrightarrow b } \right| < \left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right|\end{array}\)