Giải bài 4.12 trang 51 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Trên mặt phẳng, chất điểm A chịu tác động của ba lực

Quảng cáo

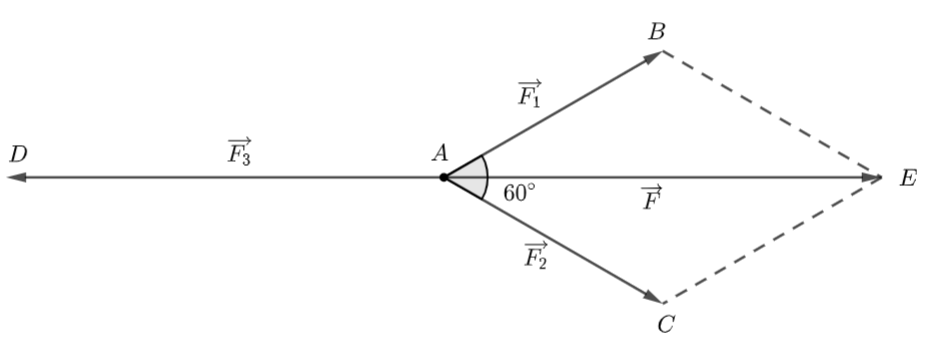
Đề bài

Trên mặt phẳng, chất điểm \(A\) chịu tác động của ba lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) và ở trạng thái cân bằng. Góc giữa hai vectơ \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} \) bằng \({60^ \circ }.\) Tính độ lớn của \(\overrightarrow {{F_3}} ,\) biết rằng \(\left| {\overrightarrow {{F_1}} } \right| = \left| {\overrightarrow {{F_2}} } \right| = 2\sqrt 3 N.\)

Phương pháp giải - Xem chi tiết

- Chứng minh tứ giác \(ABEC\) là hình thoi

- Tính cạnh \(AE\): \(AE = 2.\frac{{AB\sqrt 3 }}{2} = AB\sqrt 3 \)

- Do vật ở vị trí cân bằng nên \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow F } \right| = AE\)

Lời giải chi tiết

Giả sử \(\overrightarrow {AB} ,\,\,\overrightarrow {AC} ,\,\,\overrightarrow {AD} \) lần lượt biểu thị cho các lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} ,\,\,\overrightarrow {{F_3}} \) và vectơ \(\overrightarrow {AE} \) biểu thị cho hợp lực của hai lực \(\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} \)

Ta có: tứ giác \(ABEC\) là hình bình hành

mặt khắc \(\widehat {BAC} = {60^ \circ }\)

nên tứ giác \(ABEC\) là hình thoi

\( \Rightarrow \) \(\Delta ABC\) là tam giác đều

\( \Rightarrow \) \(AE = 2.\frac{{2\sqrt 3 .\sqrt 3 }}{2} = 6\,\,(N)\)

Do vật ở vị trí cân bằng nên hai lực \(\overrightarrow F \) và \(\overrightarrow {{F_3}} \) có cùng cường độ và ngược chiều nhau

\( \Rightarrow \) \(\left| {\overrightarrow {F{}_3} } \right| = \left| {\overrightarrow F } \right| = AE = 6\,\,(N)\)