Giải bài 4.10 trang 51 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

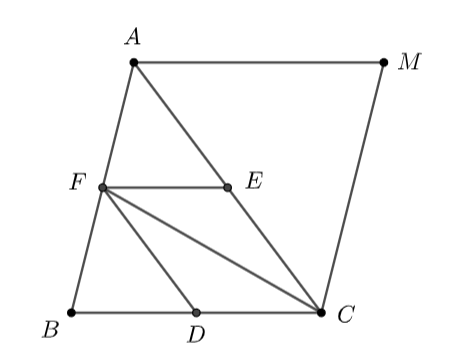
Đề bài

Cho tam giác \(ABC.\) Gọi \(D,\,\,E,\,\,F\) theo thứ tự là trung điểm của các cạnh \(BC,\,\,CA,\,\,AB.\)

a) Xác định vectơ \(\overrightarrow {AF}  - \overrightarrow {BD}  + \overrightarrow {CE} \)

b) Xác định điểm \(M\) thỏa mãn \(\overrightarrow {AF}  - \overrightarrow {BD}  + \overrightarrow {CE}  = \overrightarrow {MA} .\)

c) Chứng minh rằng \(\overrightarrow {MC}  = \overrightarrow {AB} .\)

Lời giải chi tiết

a)      Ta có: \(DF\) là đường trung bình của \(\Delta ABC\)

\( \Rightarrow \) \(\overrightarrow {CE}  = \overrightarrow {DF} \)

\( \Rightarrow \) tứ giác \(CDFE\) là hình bình hành.

Ta có: \(D\) và \(F\) lần lượt là trung điểm của \(BC\) và \(AB\)

\( \Rightarrow \) \(\overrightarrow {AF}  = \overrightarrow {FB} ,\) \(\overrightarrow {BD}  = \overrightarrow {DC} \) 

Ta có: \(\overrightarrow {AF}  - \overrightarrow {BD}  + \overrightarrow {CE}  = \overrightarrow {AF}  + \overrightarrow {CD}  + \overrightarrow {CE}  = \overrightarrow {AF}  + \overrightarrow {CF}  = \overrightarrow {CF}  + \overrightarrow {FB}  = \overrightarrow {CB} \)

b)     Theo câu a, ta có: \(\overrightarrow {AF}  - \overrightarrow {BD}  + \overrightarrow {CE}  = \overrightarrow {CB} \)

mặt khác \(\overrightarrow {AF}  - \overrightarrow {BD}  + \overrightarrow {CE}  = \overrightarrow {MA} .\)

nên \(\overrightarrow {CB}  = \overrightarrow {MA} \)

\( \Rightarrow \) tứ giác \(ABCM\) là hình bình hành

\( \Rightarrow \) \(M\) là điểm đối xứng với \(B\) qua \(E\)

c)      Theo câu b, ta có: tứ giác \(ABCM\) là hình bình hành

\( \Rightarrow \) \(\overrightarrow {MC}  = \overrightarrow {AB} .\)