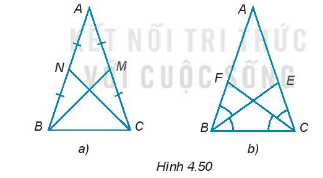
Giải bài 4.45 trang 69 sách bài tập toán 7 - Kết nối tri thức với cuộc sống

Đề bài

Cho ABC là tam giác cân tại đỉnh A. Chứng minh rằng:

a) Hai đường trung tuyến BM, CN bằng nhau (H.4.50a).

b) Hai đường phân giác BE, CF bằng nhau (H.4.50b) 

Lời giải chi tiết

a) Ta có: \(AM = \dfrac{{AC}}{2}; AN=\dfrac{{AB}}{2}\).

Mà tam giác ABC cân tại A nên AB = AC.

\(\Rightarrow AM=AN\)

Xét \(\Delta ABM\) và \(\Delta ACN\) có:

AB = AC

\(\begin{array}{l}AM = AN\\\widehat A:Chung\\ \Rightarrow \Delta ABM = \Delta ACN\left( {c - g - c} \right)\\ \Rightarrow BM = CN\end{array}\)

b) Ta có: \(\widehat {ABE} = \dfrac{{\widehat {ABC}}}{2}\) (do BE là tia phân giác của góc ABC)

\(\widehat {ACF}= \dfrac{{\widehat {ACB}}}{2}\) (do CF là tia phân giác của góc ACB)

Mà tam giác ABC cân tại A nên \(\widehat {ABC}=\widehat {ACB}\)

Do đó, \(\widehat {ABE} = \widehat {ACF}\)

Xét \(\Delta ABE\) và \(\Delta ACF\) có:

\(\widehat A:Chung\\AB=AC\\\widehat {ABE} = \widehat {ACF}\\ \Rightarrow \Delta ABE = \Delta ACF\left( {g - c - g} \right)\)

\(\Rightarrow BE = CF.\) ( 2 cạnh tương ứng)