Giải bài 43 trang 122 sách bài tập toán 9 - Cánh diều tập 1Cho hình chữ nhật ABCD với AB = 10cm. Vẽ hai nửa đường tròn tâm O đường kính AB và tâm O’ đường kính CD cắt nhau tại P, Q. Biết rằng đường tròn tâm H đường kính PQ tiếp xúc với AB và CD (Hình 47). Tính diện tích phần chung của hai nửa đường tròn (O), (O’). Quảng cáo
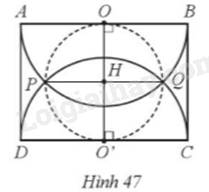
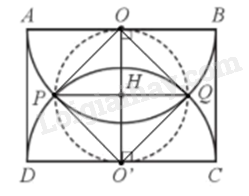
Đề bài Cho hình chữ nhật ABCD với AB = 10cm. Vẽ hai nửa đường tròn tâm O đường kính AB và tâm O’ đường kính CD cắt nhau tại P, Q. Biết rằng đường tròn tâm H đường kính PQ tiếp xúc với AB và CD (Hình 47). Tính diện tích phần chung của hai nửa đường tròn (O), (O’).
Phương pháp giải - Xem chi tiết Bước 1: Chứng minh OPO’Q là hình vuông và cạnh hình vuông. Bước 2: Diện tích cần tìm = diện tích phần tạo bởi dây PQ và cung nhỏ PQ của (O) + diện tích phần tạo bởi dây PQ và cung nhỏ PQ của (O’). Trong đó: Diện tích phần tạo bởi dây PQ và cung nhỏ PQ của (O) = diện tích quạt tròn OPQ – diện tích tam giác OPQ. Diện tích phần tạo bởi dây PQ và cung nhỏ PQ của (O’) = diện tích quạt tròn O’PQ – diện tích tam giác O’PQ. Lời giải chi tiết
Ta có: O là tâm đường tròn đường kính AB nên \(OA = OB = OP = OQ = \frac{{AB}}{2} = \frac{{10}}{2} = 5\)cm. Ta lại có: O’ là tâm đường tròn đường kính CD nên \(O'C = O'D = O'P = O'Q = \frac{{CD}}{2}\) Mà \(AB = CD\) (do ABCD là hình chữ nhật), suy ra \(OP = OQ = O'P = O'Q\). Có: AB, CD tiếp xúc với (H), \(OH \bot AB\)tại O tại O’, do đó O và O’ là tiếp điểm của 2 tiếp tuyến AB và CD của (H), hay \(O \in (H),O' \in (H)\). Diện tích tam giác OPQ là: \(\frac{1}{2}OP.OQ = \frac{1}{2}5.5 = \frac{{25}}{2}\)(cm2) Diện tích hình quạt tròn OPQ của (O) là \(\frac{{\pi {{.5}^2}.90}}{{360}} = \frac{{25\pi }}{4}\)(cm2) Diện tích hình tạo bởi dây PQ và cung nhỏ PQ của (O) là: \(\frac{{25\pi }}{4} - \frac{{25}}{2} = \frac{{25}}{4}\left( {\pi - 2} \right)\)(cm2) Diện tích tam giác O’PQ là: \(\frac{1}{2}OP.OQ = \frac{1}{2}5.5 = \frac{{25}}{2}\)(cm2) Diện tích hình quạt tròn O’PQ của (O’) là \(\frac{{\pi {{.5}^2}.90}}{{360}} = \frac{{25\pi }}{4}\) (cm2) Diện tích hình tạo bởi dây PQ và cung nhỏ PQ của (O’) là: \(\frac{{25\pi }}{4} - \frac{{25}}{2} = \frac{{25}}{4}\left( {\pi - 2} \right)\) (cm2) Vậy diện tích phần chung của 2 nửa đường tròn (O) và (O’) là: \(2.\frac{{25}}{4}\left( {\pi - 2} \right) = \frac{{25}}{2}\left( {\pi - 2} \right)\) (cm2)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
