Giải bài 4.15 trang 54 sách bài tập toán 10 - Kết nối tri thức với cuộc sốngCho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Quảng cáo
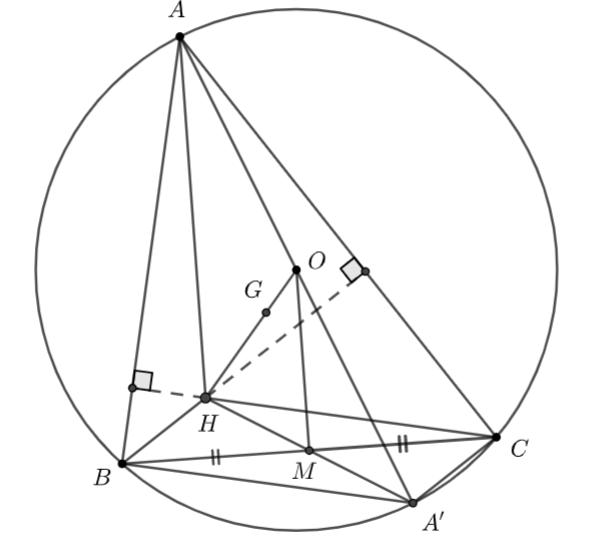
Đề bài Cho tam giác \(ABC\) có trực tâm \(H,\) trọng tâm \(G\) và tâm đường tròn ngoại tiếp \(O.\) a) Gọi \(M\) là trung điểm của \(BC.\) Chứng minh rằng \(\overrightarrow {AH} = 2\overrightarrow {OM} .\) b) Chứng minh rằng \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} .\) c) Chứng minh rằng ba điểm \(G,\,\,H,\,\,O\) cùng thuộc một đường thẳng. Phương pháp giải - Xem chi tiết - Chứng minh tứ giác \(ABHC\) là hình bình hành - Chứng minh \(MO\) là đường trung bình của \(\Delta AA'H\) - Chứng minh \(\overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {OM} \) từ đó rút ra kết luận \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OH} .\) - Chứng minh \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} .\) - Chứng minh \(\overrightarrow {OH} \) và \(\overrightarrow {OG} \) cùng phương Lời giải chi tiết
a) Xét \((O)\) có: \(\widehat {ABA'} = \widehat {ACA'} = {90^ \circ }\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow A'C \bot AC\) và \(A'B \bot AB\) (1) Ta có: \(H\) là trực tâm của tam giác \(ABC.\) \( \Rightarrow BH \bot AC\) và \(CH \bot AB\) (2) Từ (1) và (2) \( \Rightarrow \) \(BH\)//\(A'C\) và \(A'B\)//\(CH.\) Xét tứ giác \(ABHC\) có: \(BH\)//\(A'C\) và \(A'B\)//\(CH\) \( \Rightarrow \) tứ giác \(ABHC\) là hình bình hành (dấu hiệu nhận biết) \( \Rightarrow \overrightarrow {BH} = \overrightarrow {A'C} \) Ta có: tứ giác \(ABHC\) là hình bình hành nên \(M\) là trung điểm của \(A'H\) Xét \(\Delta AA'H\) có: \(M\) là trung điểm của \(A'H\) \(O\) là trung điểm của \(AA'\) \( \Rightarrow \) \(MO\) là đường trung bình của \(\Delta AA'H\) \( \Rightarrow \) \(MO\)//\(AH\) và \(2MO = AH\) \( \Rightarrow \) hai vectơ \(\overrightarrow {MO} ,\,\,\overrightarrow {AH} \) cùng hướng và \(2\overrightarrow {OM} = \overrightarrow {AH} .\) b) Ta có: \(\overrightarrow {OB} + \overrightarrow {OC} = \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MC} } \right) = 2\overrightarrow {OM} + \left( {\overrightarrow {MB} + \overrightarrow {MC} } \right) = 2\overrightarrow {OM} \) Ta có: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OA} + 2\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {AH} = \overrightarrow {OH} \) (3) c) Ta có: \(G\) là trọng tâm của \(\Delta ABC\) nên \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} .\) (4) Từ (3) và (4) \( \Rightarrow \overrightarrow {OH} = 3\overrightarrow {OG} \) \( \Rightarrow \overrightarrow {OH} \) và \(\overrightarrow {OG} \) cùng phương hay ba điểm \(G,\,\,H,\,\,O\) cùng thuộc một đường thẳng.
|




















Danh sách bình luận