Giải bài 4.20 trang 55 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Đề bài

Cho tam giác \(ABC.\)

a)      Tìm điểm \(K\) thỏa mãn \(\overrightarrow {KA}  + 2\overrightarrow {KB}  + 3\overrightarrow {KC}  = \overrightarrow 0 \)

b)     Tìm tập hợp các điểm \(M\) thỏa mãn \(\left| {\overrightarrow {MA}  + 2\overrightarrow {MB}  + 3\overrightarrow {MC} } \right| = \left| {\overrightarrow {MB}  - \overrightarrow {MC} } \right|\)

Lời giải chi tiết

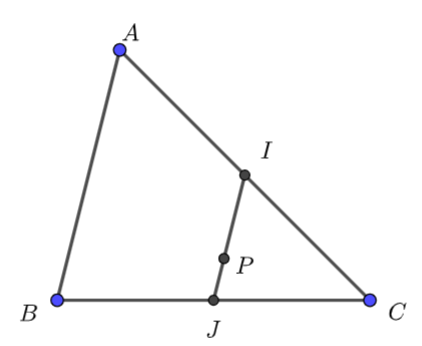
a)      Giả sử tìm được điểm \(K\) thỏa mãn \(\overrightarrow {KA}  + 2\overrightarrow {KB}  + 3\overrightarrow {KC}  = \overrightarrow 0 \)

Gọi \(I\) là trung điểm của \(AC\), \(J\) là trung điểm của \(BC\).

Ta có: \(\overrightarrow {KA}  + 2\overrightarrow {KB}  + 3\overrightarrow {KC}  = \left( {\overrightarrow {KA}  + \overrightarrow {KC} } \right) + 2\left( {\overrightarrow {KB}  + \overrightarrow {KC} } \right) = 2\overrightarrow {KI}  + 4\overrightarrow {KJ} \)     (1)

Lấy điểm \(P\) trên cạnh \(IJ\) sao cho \(\overrightarrow {PI}  + 2\overrightarrow {PJ}  = \overrightarrow 0 \)

Ta có: \(2\overrightarrow {KI}  + 4\overrightarrow {KJ}  = 2\left( {\overrightarrow {KP}  + \overrightarrow {PI} } \right) + 4\left( {\overrightarrow {KP}  + \overrightarrow {PJ} } \right) = 6\overrightarrow {KP} \)        (2)

Từ (1) và (2) \( \Rightarrow \) \(\overrightarrow {KA}  + 2\overrightarrow {KB}  + 3\overrightarrow {KC}  = 6\overrightarrow {KP} \)

Mặt khác \(\overrightarrow {KA}  + 2\overrightarrow {KB}  + 3\overrightarrow {KC}  = \overrightarrow 0 \)

\( \Rightarrow \) \(6\overrightarrow {KP}  = \overrightarrow 0 \) \( \Leftrightarrow \) \(K \equiv P\)

Vậy điểm \(K\)  thuộc cạnh \(IJ\) sao cho \(\overrightarrow {KI}  + 2\overrightarrow {KJ}  = \overrightarrow 0 \)

b)     Ta có: \(\left| {\overrightarrow {MA}  + 2\overrightarrow {MB}  + 3\overrightarrow {MC} } \right| = \left| {\overrightarrow {MB}  - \overrightarrow {MC} } \right|\)

\( \Leftrightarrow \,\,\left| {6\overrightarrow {MP} } \right| = \left| {\overrightarrow {CB} } \right|\,\, \Leftrightarrow \,\,MP = \frac{1}{6}BC\)

\( \Rightarrow \) tập hợp điểm \(M\) cần tìm là đường tròn tâm \(P\), bán kính bằng \(\frac{{BC}}{6}\).