Giải bài 4 trang 7 vở thực hành Toán 9 tập 2Vẽ đồ thị của các hàm số sau: a) (y = 3{x^2}); b) (y = - frac{1}{3}{x^2}). Tổng hợp đề thi giữa kì 2 lớp 9 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - KHTN Quảng cáo
Đề bài Vẽ đồ thị của các hàm số sau: a) \(y = 3{x^2}\); b) \(y = - \frac{1}{3}{x^2}\). Phương pháp giải - Xem chi tiết Cách vẽ đồ thị hàm số \(y = a{x^2}\left( {a \ne 0} \right)\): + Lập bảng ghi một số cặp giá trị tương ứng của x và y. + Trong mặt phẳng tọa độ Oxy, biểu diễn các cặp điểm (x; y) trong bảng giá trị trên và nối chúng lại để được một đường cong là đồ thị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\). Lời giải chi tiết a) Lập bảng một số giá trị tương ứng giữa x và y:
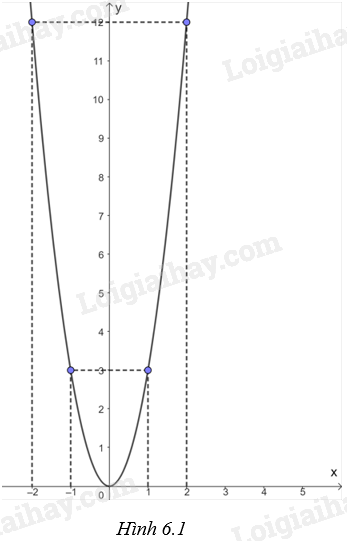
Từ đó vẽ được đồ thị hàm số \(y = 3{x^2}\) như Hình 6.1.
b) Lập bảng một số giá trị tương ứng giữa x và y:
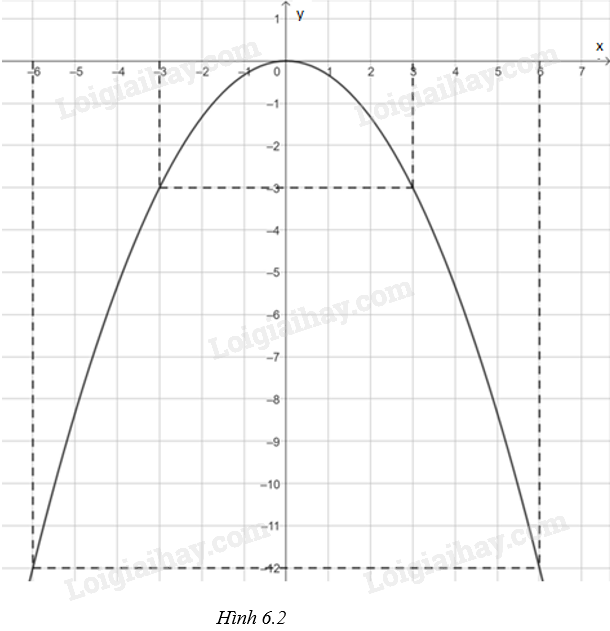
Từ đó vẽ được đồ thị của hàm số \(y = - \frac{1}{3}{x^2}\) như Hình 6.2.
|






















Danh sách bình luận