Giải bài 3.46 trang 44 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

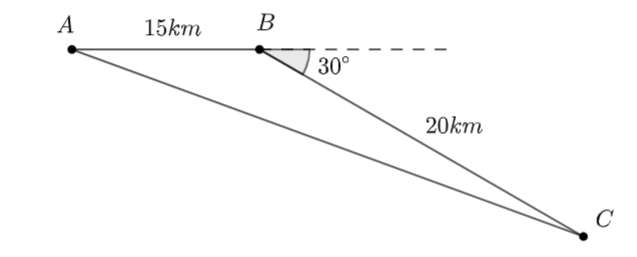
Đề bài

Trên biển, một tàu cá xuất phát từ cảng A, chạy về phương đông 15 km tới B, rồi chuyển sang hướng \(E{30^ \circ }S\) chạy tiếp 20 km nữa tới đảo C.

a) Tính khoảng cách từ A đến C (làm tròn đến hàng đơn vị, theo đơn vị ki lô mét).

b) Xác định hướng từ A tới C (làm tròn đến hàng đơn vị, theo đơn vị độ).

Lời giải chi tiết

a) Ta có: \(\widehat {ABC} = {180^ \circ } - {30^ \circ } = {150^ \circ }.\)

Khoảng cách từ A đến C là:

Áp dụng định lý cosin, ta có:

\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} + 2AB.BC.\cos \widehat {ABC}\\ \Rightarrow \,\,A{C^2} = 225 + 400 - 2.15.20.\cos {150^ \circ }\\ \Rightarrow \,\,A{C^2} \approx 1144.6\\ \Rightarrow \,\,AC \approx 33.8\end{array}\)

b) Áp dụng định lý sin, ta có:

\(\begin{array}{l}\frac{{AC}}{{\sin \widehat {ABC}}} = \frac{{BC}}{{\sin \widehat A}}\,\, \Leftrightarrow \,\,\frac{{33.8}}{{\sin {{150}^ \circ }}} = \frac{{20}}{{\sin \widehat A}}\\ \Leftrightarrow \,\,\sin \widehat A = \frac{{20.\sin {{150}^ \circ }}}{{33.8}} \approx 0.296\\\,\, \Leftrightarrow \widehat A = {17^ \circ }.\end{array}\)

Vậy từ A tới C là hướng \(E{17^ \circ }S.\)