Bài 3.45 trang 132 SBT hình học 12Giải bài 3.45 trang 132 sách bài tập hình học 12. Cho hai đường thẳng... Quảng cáo
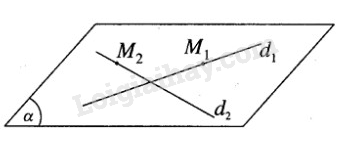
Đề bài Cho hai đường thẳng d1: \(\dfrac{{x - 1}}{2} = \dfrac{{y + 2}}{{ - 3}} = \dfrac{{z - 5}}{4}\) và d2: \(\left\{ {\begin{array}{*{20}{c}}{x = 7 + 3t}\\{y = 2 + 2t}\\{z = 1 - 2t}\end{array}} \right.\) a) Chứng minh rằng d1 và d2 cùng nằm trong một mặt phẳng \((\alpha )\). b) Viết phương trình của \((\alpha )\). Phương pháp giải - Xem chi tiết Sử dụng vị trí tương đối giữa hai đường thẳng. Xem chi tiết tại đây. Lời giải chi tiết
a) Ta có \(\overrightarrow {{u_{{d_1}}}} = \left( {2; - 3;4} \right)\) và \(\overrightarrow {{u_{{d_2}}}} = (3;2; - 2)\) \(\overrightarrow n = \left[ {\overrightarrow {{u_{{d_1}}}} ,\overrightarrow {{u_{{d_2}}}} } \right] = ( - 2;16;13)\) Lấy điểm M1(1; -2; 5) trên d1 và điểm M2(7;2;1) trên d2. Ta có \(\overrightarrow {{M_1}{M_2}} = (6;4; - 4)\); \(\overrightarrow n .\overrightarrow {{M_1}{M_2}} = - 12 + 64 - 52 = 0\) Suy ra \({d_1}\) và \({d_2}\) cùng nằm trong mặt phẳng \((\alpha )\) b) Mặt phẳng \((\alpha )\) chứa \({M_1}\) và có vecto pháp tuyến là \(\overrightarrow n \) , vậy phương trình của \((\alpha )\) là: \(– 2(x – 1) +16(y + 2) + 13(z – 5) = 0\) hay \(2x – 16y – 13z + 31 = 0\). Loigiaihay.com
|




















Danh sách bình luận