Giải Bài 33 trang 78 sách bài tập toán 7 - Cánh diều

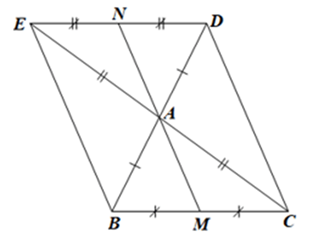
Đề bài

Cho tam giác ABC. Trên tia đối của tia AB, AC lần lượt lấy các điểm D và E sao cho AD = AB và AE = AC. Gọi M, N lần lượt là trung điểm của BC và DE.

Chứng minh:

a) ∆ABC = ∆ADE;

b) DE = BC và DE song song với BC;

c) ∆AEN = ∆ACM;

d) M, A, N thẳng hàng.

Lời giải chi tiết

 

a) Xét ΔABC và ΔADE có:

AB = AD (giả thiết),

\(\widehat {BAC} = \widehat {DA{\rm{E}}}\) (hai góc đối đỉnh),

AC = AE (giả thiết).

Do đó ΔABC = ∆ADE (c.g.c).

Vậy ΔABC = ∆ADE.

b) Vì ∆ABC = ∆ADE (chứng minh câu a)

Suy ra BC = DE (hai cạnh tương ứng), \(\widehat {ACB} = \widehat {AED}\) (hai góc tương ứng).

Mặt khác \(\widehat {ACB},\widehat {AED}\) là hai góc ở vị trí so le trong.

Suy ra DE // BC.

Vậy DE = BC và DE song song với BC.

c) Ta có: \(EN = \frac{{DE}}{2};MC = \frac{{BC}}{2};DE = BC\) nên EN = MC

Xét ∆AEN và ∆ACM có:

AE = AC (giả thiết),

\(\widehat {NEA} = \widehat {MCA}\) (do \(\widehat {AED} = \widehat {ACB}\))

EN = CM (chứng minh trên),

Suy ra ∆AEN = ∆ACM (c.g.c)

Vậy ∆AEN = ∆ACM.

d) Do ∆AEN = ∆ACM (chứng minh câu c).

Nên \(\widehat {NAE} = \widehat {MAC}\) (hai góc tương ứng)

Ta có: \(\widehat {NAM} = \widehat {NAE} + \widehat {EAM} = \widehat {MAC} + \widehat {EAM}\)

 Mà \(\widehat {MAC} + \widehat {EAM} = \widehat {EAC} = 180^\circ \) (hai góc kề bù)

Do đó \(\widehat {NAM} = {180^o}\)

Suy ra M, A, N thẳng hàng

Vậy M, A, N thẳng hàng.