Giải Bài 33 trang 114 sách bài tập toán 7 tập 1 - Cánh diềuQuan sát Hình 43, biết Quảng cáo
Đề bài Quan sát Hình 43, biết \(\widehat {MNO} = \widehat {AOB} = \widehat {BQM} = 90^\circ ,\widehat {ABO} = 50^\circ \). Tìm số đo mỗi góc NMQ, BMQ, MAN.
Phương pháp giải - Xem chi tiết Sử dụng Dấu hiệu nhận biết 2 đường thẳng song song và tính chất 2 đường thẳng song song. Lời giải chi tiết Vì \(MN \bot OA; OB \bot OA \) nên \(MN //OB\) (cùng vuông góc với OA) Do đó \(\widehat {NMQ}=\widehat{MQB}\) (2 góc so le trong); \( \widehat {NMA}=\widehat{OBA}\) (2 góc đồng vị) Mà \(\widehat{MQB}= 90^\circ ; \widehat{OBA}=50^0\) nên \(\widehat {NMQ}=90^0;\widehat {NMA}=50^0 \); Vì \(\widehat {BMQ}+\widehat {QMN}+\widehat {NMA}=180^0\) nên \(\widehat {BMQ}=180^0-90^0-50^0= 40^\circ \). Vì \(NO \bot OB; MQ \bot OB \) nên \(NO//MQ\) (cùng vuông góc với OB). Do đó \(\widehat {MAN} = \widehat {BMQ} = 40^\circ \) (hai góc đồng vị).
|














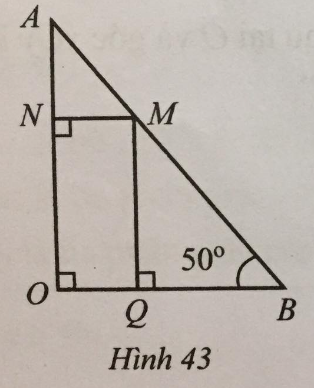






Danh sách bình luận