Giải Bài 35 trang 115 sách bài tập toán 7 tập 1 - Cánh diềuQuan sát Hình 45. Cho OD vuông góc với CC’ tại O, Quảng cáo
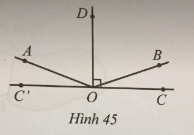
Đề bài Quan sát Hình 45. Cho OD vuông góc với CC’ tại O, \(\widehat {AOC} = 160^\circ ,{\rm{ }}\widehat {AOB} - \widehat {BOC} = 120^\circ \). a) Tính số đo mỗi góc AOB, BOC. b) Tia OD có là tia phân giác của góc AOB hay không? c) So sánh hai góc AOC và BOC’.
Phương pháp giải - Xem chi tiết a) Tính số đo mỗi góc dựa vào hai góc AOB và BOC kề nhau. b) Muốn biết tia OD có là tia phân giác của góc AOB hay không, ta tính số đo các góc được tạo bởi tia OD và tia OA, OB. c) Tính số đo của 2 góc rồi so sánh. Lời giải chi tiết a) Do hai góc AOC và BOC là hai góc kề nhau nên \(\widehat {AOB} + \widehat {BOC} = \widehat {AOC} = 160^\circ \). Mà \(\widehat {AOB} - \widehat {BOC} = 120^\circ \) nên \(\widehat {AOB} = 140^\circ \) và \(\widehat {BOC} = 20^\circ\) b) Vì \(OD \bot CC' \) nên \(\widehat {COD} = 90^\circ \). Do đó góc AOD và COD là hai góc kề nhau nên \(\widehat {AOD} + \widehat {COD} = \widehat {AOC}\). Suy ra: \(\widehat {AOD} = \widehat {AOC} - \widehat {COD} = 160^\circ - 90^\circ = 70^\circ \). Tương tự, ta có: \(\widehat {BOD} = \widehat {COD} - \widehat {BOC} = 90^\circ - 20^\circ = 70^\circ \). Do đó: \(\widehat {AOD} = \widehat {BOD}\). Mà OD nằm giữa hai tia OA và OB nên OD là tia phân giác của góc AOB. c) Ta có \(\widehat {BOC'} + \widehat {BOC} = 180^\circ \) (hai góc kề bù) nên \(\widehat {BOC'} = 180^\circ - \widehat {BOC} = 180^\circ - 20^\circ = 160^\circ \). Vậy \(\widehat {AOC} = \widehat {BOC'}\).
|




















Danh sách bình luận