Giải bài 3.10 trang 39 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

a) Tính khoảng cách từ vị trí xuất phát từ A đến C (làm tròn đến hàng đơn vị, theo đơn vị đo ki lô mét).

Quảng cáo

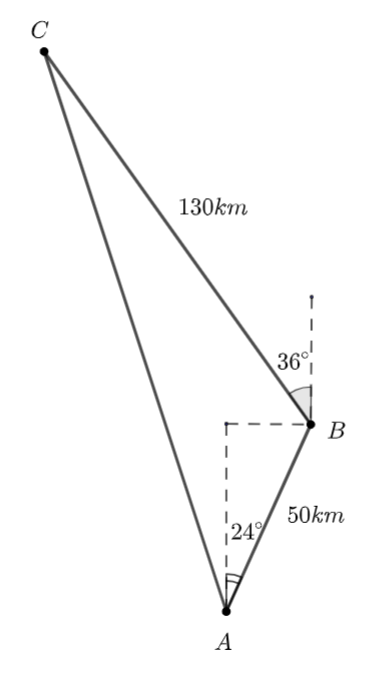
Đề bài

Một tàu các xuất phát từ đảo \(A,\) chạy 50 km theo hướng \(N{24^ \circ }E\) đến đảo \(B\) để lấy thêm ngư cụ, rồi chuyển hướng \(N{36^ \circ }W\) chạy tiếp 130 km đến ngư trường \(C.\)

a) Tính khoảng cách từ vị trí xuất phát từ A đến C (làm tròn đến hàng đơn vị, theo đơn vị đo ki lô mét).

b) Tìm hướng từ A đến C ( đơn vị đến hàng đơn vị, theo đơn vị độ).

Phương pháp giải - Xem chi tiết

- Tính \(\widehat B\)

- Áp dụng định lý cosin để tính độ dài \(AC:\) \(A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos B\)

- Tính \(\widehat {CAB}\) dựa vào định lý sin \(\frac{{CB}}{{\sin CAB}} = \frac{{AC}}{{\sin ABC}}\)

- Tính góc AC chếch về hương tây

Lời giải chi tiết

Ta có: \(\widehat B = \left( {{{90}^ \circ } - {{36}^ \circ }} \right) + \left( {{{90}^ \circ } - {{24}^ \circ }} \right) = {120^ \circ }.\)

a) Độ dài đoạn thẳng AC là:

Áp dụng định lý cosin, ta có:

\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} - 2AB.BC.\cos B\\A{C^2} = {50^2} + {130^2} - 2.50.130.\cos {120^ \circ }\\A{C^2} = 2500 + 16900 + 6500 = 25900\\ \Rightarrow \,\,AC = \sqrt {25900} = 10\sqrt {259} \approx 161\,\,km\end{array}\)

b) Áp dụng định lý sin, ta có:

\(\begin{array}{l}\frac{{CB}}{{\sin CAB}} = \frac{{AC}}{{\sin ABC}}\,\, \Rightarrow \,\,\frac{{130}}{{\sin CAB}} = \frac{{161}}{{\sin {{120}^ \circ }}}\\ \Rightarrow \,\,\sin CAB = \frac{{130.\sin {{120}^ \circ }}}{{161}} \approx 0,6993\\ \Rightarrow \,\,\widehat {CAB} \approx {44^ \circ }\end{array}\)

Góc AC chếch về hướng tây một góc \({44^ \circ } - {24^ \circ } = {20^ \circ }.\)

Vậy hướng từ A đến C là: \(N{20^ \circ }W\)