Trang chủ

Giải bài 3.12 trang 39 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Một cây cổ thụ mạc thẳng đứng bên lề một con dốc có độ dốc 10 so với phương nằm ngang. Từ một điểm dưới chân dốc, cách gốc cây 31 m người ta nhìn đỉnh ngọn cây dưới một góc 40 so với phương nằm ngang. Hãy tính chiều cao của cây.

Quảng cáo

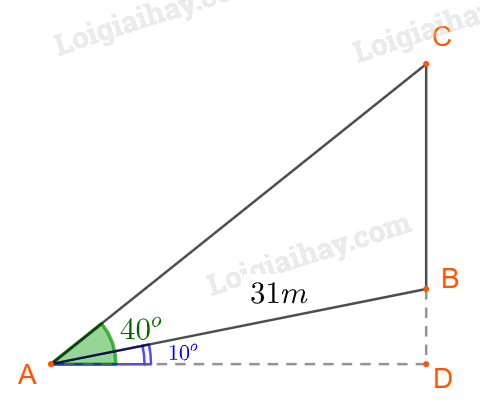
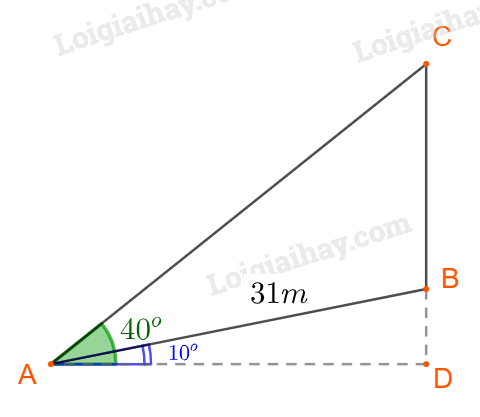
Đề bài

Một cây cổ thụ mạc thẳng đứng bên lề một con dốc có độ dốc \({10^ \circ }\) so với phương nằm ngang. Từ một điểm dưới chân dốc, cách gốc cây 31 m người ta nhìn đỉnh ngọn cây dưới một góc \({40^ \circ }\) so với phương nằm ngang. Hãy tính chiều cao của cây.

Phương pháp giải - Xem chi tiết

- Tính \(\widehat {BAC}\) và \(\widehat {ACB}\)

- Áp dụng định lý sin, tính cạnh \(BC:\frac{{BC}}{{\sin BAC}} = \frac{{AB}}{{\sin ACB}}\)

Lời giải chi tiết

Giả sử con dốc là AB, gốc cây đặt tại B, chiều cao cây cổ thụ là đoạn CB.

Khi đó ta có: \( \widehat {BAD} = {10^ \circ },\, \widehat {CAD} = {40^ \circ }\) và \(AB=31m\)

Xét \(\Delta ADC\) vuông tại \(D\) có: \(\widehat {ACB} = {90^ \circ } - \widehat {DAC} = {90^ \circ } - {40^ \circ } = {50^ \circ }.\)

Ta có: \(\widehat {CAB} = \widehat {DAC} - \widehat {DAB} = {40^ \circ } - {10^ \circ } = {30^ \circ }.\)

Chiều cao của cây là:

Áp dụng định lý sin, ta có:

\(\begin{array}{l}\frac{{BC}}{{\sin BAC}} = \frac{{AB}}{{\sin ACB}}\,\, \Rightarrow \,\,BC = \frac{{AB.\sin BAC}}{{\sin ACB}}\\ \Rightarrow \,\,BC = \frac{{31.\sin {{30}^ \circ }}}{{\sin {{50}^ \circ }}} \approx 20,23\,\,m\end{array}\)