Bài 29 trang 111 Vở bài tập toán 6 tập 2

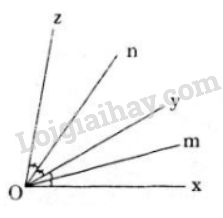
Đề bài

Cho hai tia \(Oy,Oz\) cùng nằm trên một nửa mặt phẳng có bờ chứa tia \(Ox.\) Biết: \(\widehat{ xOy}=30^0,\) \(\widehat{ xOz}=80^0.\) Vẽ tia phân giác \(Om\) của \(\widehat {xOy}\). Vẽ tia phân giác \(On\) của \(\widehat {yOz}\). Tính \(\widehat {mOn}\) 

Lời giải chi tiết

Vì hai tia \(Oy, Oz\) cùng nằm trên nửa mặt phẳng bờ chứa tia \(Ox\) mà 

\(\widehat{ xOy}\)<  \(\widehat{ xOz}\) \((30^0<80^0)\) nên tia \(Oy\) nằm giữa hai tia \(Ox, Oz.\)

Do đó  \(\widehat{ xOy}\)+ \(\widehat{ yOz}\)= \(\widehat{ xOz}\)  

Suy ra  \(\widehat{ yOz}=\widehat{ xOz}-\widehat{ xOy}\)\(= 80^0-50^0=30^0\) 

Ta có tia \(Om\) là tia phân giác của góc \(xOy\) nên: \(\widehat {xOm} = \widehat {mOy} \)\(= \dfrac{{\widehat {xOy}}}{2} = \dfrac{{{{30}^0}}}{2} = {15^0}\)

Tia \(On\) là tia phân giác của góc \(yOz\) nên: \(\widehat {yOn} = \widehat {nOz} = \dfrac{{\widehat {yOz}}}{2} \)\(= \dfrac{{{{50}^0}}}{2} = {25^0}\)

Vì \(\widehat {nOz}<\widehat {xOz}\) (vì \(25^0<80^0)\) nên tia \(On\) nằm giữa hai tia \(Ox\) và \(Oz\).

Do đó  \(\widehat{ xOn}\)+ \(\widehat{ nOz}\)= \(\widehat{ xOz}\)  

Suy ra  \(\widehat{ xOn}=\widehat{ xOz}-\widehat{ zOn}\)\(= 80^0-25^0=55^0\) 

Vì \(\widehat {mOx}<\widehat {xOn}\) (vì \(15^0<55^0)\) nên tia \(Om\) nằm giữa hai tia \(Ox\) và \(On\).

Do đó  \(\widehat{ xOm}\)+ \(\widehat{ nOm}\)= \(\widehat{ xOn}\)  

Suy ra  \(\widehat{ mOn}=\widehat{ xOn}-\widehat{ xOm}\)\(= 55^0-15^0=40^0\)

Loigiaihay.com