Bài 21 trang 52 Vở bài tập toán 8 tập 2

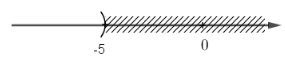
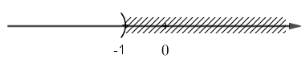
LG a

 \(\dfrac{{15 - 6x}}{3} > 5\)    

Phương pháp giải:

 Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.

Lời giải chi tiết:

Ta có

\(\eqalign{
& {{15 - 6x} \over 3} > 5 \cr  
& \Leftrightarrow 15 - 6x > 5.3 \cr 
& \Leftrightarrow 15 - 6x > 15  \cr 
& \Leftrightarrow - 6x > 0 \cr 
& \Leftrightarrow x < 0 \cr} \)

Vậy nghiệm là \(x < 0\) và được biểu diễn trên trục số như sau:

LG b

\(\dfrac{{8 - 11x}}{4} < 13\) 

Phương pháp giải:

 Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.

Lời giải chi tiết:

Ta có                                        

\(\eqalign{
& {{8 - 11x} \over 4} < 13 \cr 
& \Leftrightarrow 8 - 11x < 13.4  \cr 
& \Leftrightarrow - 11x < 44 \cr 
& \Leftrightarrow x > - 4 \cr} \)

Vậy nghiệm là \(x >  - 4\) và được biểu diễn trên trục số như sau: 

LG c

\(\dfrac{1}{4}\left( {x - 1} \right) < \dfrac{{x - 4}}{6}\)     

Phương pháp giải:

 Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.

Lời giải chi tiết:

Ta có

\(\eqalign{
& {1 \over 4}\left( {x - 1} \right) < {{x - 4} \over 6} \cr 
& \Leftrightarrow 12.{1 \over 4}\left( {x - 1} \right) < 12.{{x - 4} \over 6} \cr 
& \Leftrightarrow 3x - 3 < 2x - 8  \cr 
& \Leftrightarrow x < - 5 \cr} \) 

Vậy nghiệm là \( x <  - 5\) và được biểu diễn trên trục số như sau:

LG d

\(\dfrac{{2 - x}}{3} < \dfrac{{3 - 2x}}{5}\) 

Phương pháp giải:

 Áp dụng: Quy tắc chuyển vế và quy tắc nhân hai vế với một số.

Lời giải chi tiết:

Ta có

\(\eqalign{
& {{2 - x} \over 3} < {{3 - 2x} \over 5} \cr 
& \Leftrightarrow 10 - 5x < 9 - 6x  \cr 
& \Leftrightarrow x < - 1 \cr} \)

Vậy nghiệm là \(x <  - 1\) và được biểu diễn trên trục số như sau:  

Loigiaihay.com