Giải bài 19: Hình tam giác, hình tứ giác. Hình chữ nhật, hình vuông (tiết 3) trang 52, 53 vở bài tập Toán 3 - Kết nối tri thức với cuộc sốngCho ABCD là hình chữ nhật có BC = 20 cm, CD = 50 cm. Một con kiến đang ở điểm A ... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Câu 1 Viết số thích hợp vào chỗ chấm.
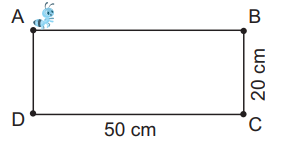
Cho ABCD là hình chữ nhật có BC = 20 cm, CD = 50 cm. Một con kiến đang ở điểm A (như hình vẽ). a) Nếu con kiến muốn bò đến điểm B theo cạnh AB thì phải bò một đoạn đường dài ....... cm. b) Nếu con kiến muốn bò đến điểm D theo cạnh AD thì phải bò một đoạn đường dài ....... cm. c) Nếu con kiến muốn bò đến điểm C theo đường gấp khúc ABC thì phải bò một đoạn đường dài ..... cm. Phương pháp giải: a) Đoạn đường con kiến bò đến điểm B theo cạnh AB là chiều dài của hình chữ nhật b) Đoạn đường con kiến bò đến điểm D theo cạnh AD là chiều rộng hình chữ nhật c) Độ dài đường gấp khúc ABC bằng tổng chiều dài cộng với chiều rộng Lời giải chi tiết: a) Nếu con kiến muốn bò đến điểm B theo cạnh AB thì phải bò một đoạn đường dài 50 cm. b) Nếu con kiến muốn bò đến điểm D theo cạnh AD thì phải bò một đoạn đường dài 20 cm. c) Nếu con kiến muốn bò đến điểm C theo đường gấp khúc ABC thì phải bò một đoạn đường dài 70 cm. Câu 2 Viết số thích hợp vào chỗ chấm.
Rùa và Ốc sên thi chạy. Hai bạn cùng xuất phát từ điểm M chạy đến đích ở điểm N nhưng theo hai đường khác nhau. Ốc sên chạy đến đích theo cạnh MN, còn Rùa chạy đến đích theo đường gấp khúc MQPN. Biết rằng MQPN là hình chữ nhật có NP = 50 cm Đoạn đường Rùa chạy dài hơn đoạn đường Ốc sên chạy là ....... cm. Phương pháp giải: Đoạn đường Rùa chạy dài hơn đoạn đường của Ốc sên bằng 2 lần độ dài cạnh NP. Lời giải chi tiết: Ta thấy, đoạn đường Rùa chạy theo đường gấp khúc MQPN dài hơn đoạn đường Ốc sên chạy theo cạnh MN bằng 2 lần độ dài cạnh NP. Vậy đoạn đường Rùa chạy dài hơn đoạn đường Ốc sên chạy là 100 cm. Câu 3 Khoanh vào chữ đặt trước câu trả lời đúng. a) Với số lượng các que tính giống nhau nào dưới đây thì xếp được một hình vuông (không thừa que tính nào)? A. 6 que tính B. 7 que tính C. 8 que tính b) Với số lượng các que tính giống nhau nào dưới đây thì không thể xếp được một hình chữ nhật (không thừa que tính nào)? A. 6 que tính B. 7 que tính C. 10 que tính Phương pháp giải: a) Dựa vào đặc điểm của hình vuông có 4 góc vuông và 4 cạnh dài bằng nhau. b) Dựa vào đặc điểm của hình chữ nhật có 4 góc vuông và hai cạnh dài bằng nhau, hai cạnh ngắn bằng nhau để xếp que tính thành hình chữ nhật. Lời giải chi tiết: a) Để xếp que tính thành hình vuông (không thừa que nào) Với 6 que tính: chỉ xếp được hình chữ nhật Với 7 que tính: không xếp được hình vuông và hình chữ nhật nào Với 8 que tính: xếp được 1 hình vuông với độ dài mỗi cạnh là 2 que tính Chọn C. b) 7 que tính giống nhau không thể xếp được hình chữ nhật. Chọn B.
|




















Danh sách bình luận