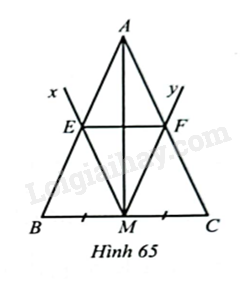
Giải bài 16 trang 65 sách bài tập toán 8 – Cánh diều

Đề bài

Cho tam giác \(ABC\) cân tại \(A\), có \(M\) là trung điểm của \(BC\). Kể tia \(Mx\) song song với \(AC\) cắt \(AB\) tại \(E\) và tia \(My\) song song với \(AB\) cắt \(AC\) tại \(F\). Chứng minh:

a)      \(EF\) là đường trung bình của tam giác \(ABC\);

b)     \(AM\) là đường trung trực của \(EF\).

Lời giải chi tiết

a)      Vì \(M\) là trung điểm của \(BC,ME//AC,MF//AB\) nên \(E,F\) lần lượt là trung điểm của \(AB.AC\). Do đó, \(EF\) là đường trung bình của tam giác \(ABC\).

b)     Ta có \(AE = \frac{{AB}}{2},AF = \frac{{AC}}{2}\) và \(AB = AC\) suy ra \(AE = AF\) (1). Lại có \(ME,MF\) là các đường trung bình của tam giác \(ABC\) nên \(ME = \frac{{AC}}{2},MF = \frac{{AB}}{2}\). Mà \(AB = AC\) suy ra \(ME = MF\) (2). Từ (1) và (2) suy ra \(AM\) là đường trung trực của \(EF\).