Giải bài 1.50 trang 33 sách bài tập toán 12 - Kết nối tri thứca) Chứng tỏ rằng nếu lợi nhuận (Pleft( x right)) là cực đại thì doanh thu biên bằng chi phí biên. b) Cho (Cleft( x right) = 16000 + 500x - 1,6{x^2} + 0,004{x^3}) là hàm chi phí và (pleft( x right) = 1700 - 7x) là hàm cầu. Hãy tìm mức sản xuất sẽ tối đa lợi nhuận. Quảng cáo
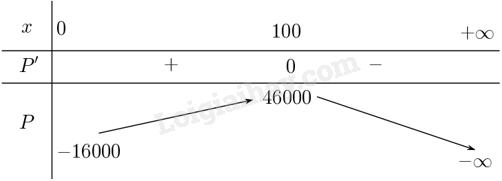
Đề bài a) Chứng tỏ rằng nếu lợi nhuận \(P\left( x \right)\) là cực đại thì doanh thu biên bằng chi phí biên. b) Cho \(C\left( x \right) = 16000 + 500x - 1,6{x^2} + 0,004{x^3}\) là hàm chi phí và \(p\left( x \right) = 1700 - 7x\) là hàm cầu. Hãy tìm mức sản xuất sẽ tối đa lợi nhuận. Phương pháp giải - Xem chi tiết Ý a: Tính hàm lợi nhuận \(P\left( x \right) = R\left( x \right) - C\left( x \right)\), tính đạo hàm và sử dụng ý nghĩa của cực đại. Ý b: Xác định công thức hàm lợi nhuận \(P\left( x \right) = x \cdot p\left( x \right) - C\left( x \right)\) và tìm giá trị lớn nhất. Lời giải chi tiết a) Ta có hàm lợi nhuận \(P\left( x \right) = R\left( x \right) - C\left( x \right)\) trong đó \(R\left( x \right)\) là doanh thu và \(C\left( x \right)\) là chi phí. Khi lợi nhuận đạt cực đại tại \({x_0}\) thì \(P'\left( {{x_0}} \right) = R'\left( {{x_0}} \right) - C'\left( {{x_0}} \right) = 0\) hay \(R'\left( {{x_0}} \right) = C'\left( {{x_0}} \right)\). Nói cách khác doanh thu biên bằng chi phí biên. b) Ta có hàm lợi nhuận \(\begin{array}{l}P\left( x \right) = x \cdot p\left( x \right) - C\left( x \right) = x\left( {1700 - 7x)} \right) - \left( {16000 + 500x - 1,6{x^2} + 0,004{x^3}} \right)\ = - 16000 + 1200x - 5,4{x^2} - 0,004{x^3}\end{array}\) Suy ra \(P'\left( x \right) = 1200 - 10,8x - 0,012{x^2}\) khi đó \(P'\left( x \right) = 0 \Leftrightarrow 1200 - 10,8x - 0,012{x^2} = 0 \Leftrightarrow x = 100\) do \(x > 0\). Lập bảng biến thiên
Vậy mức sản xuất tối đa là 100 đơn vị hàng hóa.  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
