Giải bài 1.38 trang 26 sách bài tập toán 12 - Kết nối tri thứcCho điểm (Aleft( {3;2} right)) trên mặt phẳng tọa độ. Một đường thẳng đi qua (A) cắt trục hoành tại (B), cắt trục tung tại (C) tạo thành một tam giác (OBC) nằm trong góc phần tư thứ nhất, với (O) là gốc tọa độ. a) Biết hoành độ điểm (B) là (x = t) với (t > 3). Tính diện tích tam giác (OBC) theo (t). Kí hiệu diện tích này là (Sleft( t right)). b) Khảo sát sự biến thiên của hàm số (Sleft( t right)). c) Tìm vị trí điểm (B) để diện tích tam giác (OBC) nhỏ nhất. Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Quảng cáo
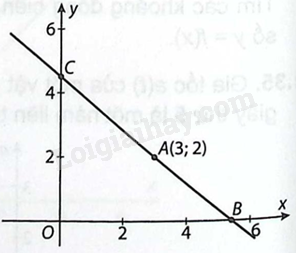
Đề bài Cho điểm \(A\left( {3;2} \right)\) trên mặt phẳng tọa độ. Một đường thẳng đi qua \(A\) cắt trục hoành tại \(B\), cắt trục tung tại \(C\) tạo thành một tam giác \(OBC\) nằm trong góc phần tư thứ nhất, với \(O\) là gốc tọa độ. a) Biết hoành độ điểm \(B\) là \(x = t\) với \(t > 3\). Tính diện tích tam giác \(OBC\) theo \(t\). Kí hiệu diện tích này là \(S\left( t \right)\). b) Khảo sát sự biến thiên của hàm số \(S\left( t \right)\). c) Tìm vị trí điểm \(B\) để diện tích tam giác \(OBC\) nhỏ nhất.
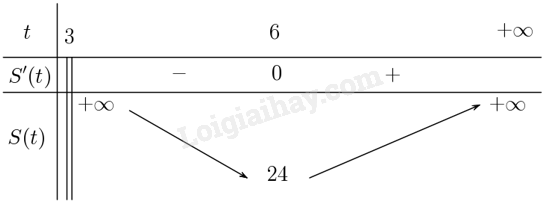
Phương pháp giải - Xem chi tiết Ý a: + Viết phương trình chính tắc đường thẳng đi qua hai điểm \(A\) và \(B\) với \(A\left( {3;2} \right);B\left( {t;0} \right)\). + Biểu diễn \(y\) theo \(x\) và \(t\), từ đó suy ra tung độ của C theo \(t\). + Tìm được diện tích \(S\left( t \right) = t \cdot {y_C}\). Ý b: Khảo sát hàm số \(S\left( t \right)\). Ý c: Từ bảng biến thiên suy ra giá trị nhỏ nhất của hàm số. Lời giải chi tiết a) Đường thẳng đi qua \(A\) và \(B\) có phương trình \(\frac{{y - 2}}{{ - 2}} = \frac{{x - 3}}{{t - 3}}\) hay \(y = 2 - \frac{2}{{t - 3}}\left( {x - 3} \right)\). Suy ra \(C\) có tung độ là \({y_C} = 2 - \frac{2}{{t - 3}}\left( {0 - 3} \right) = 2 + \frac{6}{{t - 3}}\). Diện tích tam giác \(OBC\) là \(S\left( t \right) = t \cdot {y_C} = \frac{{2{t^2}}}{{t - 3}}\). b) Xét hàm số \(S\left( t \right) = \frac{{2{t^2}}}{{t - 3}}\). Tập xác định: \(\left( {3; + \infty } \right)\). Sự biến thiên: \(S'\left( t \right) = {\left( {\frac{{2{t^2}}}{{t - 3}}} \right)^\prime } = \frac{{2{t^2} - 12t}}{{{{\left( {t - 3} \right)}^2}}}\). Khi đó \(S'\left( t \right) = 0 \Leftrightarrow \frac{{2{t^2} - 12t}}{{{{\left( {t - 3} \right)}^2}}} = 0 \Leftrightarrow 2{t^2} - 12t = 0 \Leftrightarrow t = 6\) do \(t > 3\). + Hàm số đồng biến trên khoảng \(\left( {6; + \infty } \right)\), nghịch biến trên khoảng \(\left( {3;6} \right)\). + Hàm số đạt cực tiểu tại \(t = 6\) với \({S_{CT}} = 24\). + Giới hạn tại vô cực \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty ;\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = + \infty \) + Bảng biến thiên:
c) Để diện tích tam giác \(OBC\) nhỏ nhất thì \(S\left( t \right)\) đạt giá trị nhỏ nhất. Từ bảng biến thiên suy ra, giá trị nhỏ nhất của tam giác \(OBC\) là \(24\) khi \(t = 6\) khi đó \(B\left( {0;6} \right)\)  Chia sẻ Bình luận
Quảng cáo
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
|
