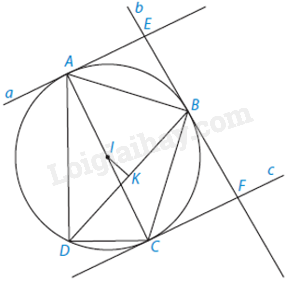
Giải bài 11 trang 135, 136 vở thực hành Toán 9 tập 2Tứ giác ABCD có hai góc đối diện B và D vuông, hai góc kia không vuông. a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Ta gọi đó là đường tròn (C). b) Gọi I và K lần lượt là trung điểm của các đường chéo AC và BD của tứ giác. Chứng minh rằng (IK bot BD). c) Kí hiệu các tiếp tuyến của đường tròn (C) tại A, B và C lần lượt là a, b và c. Giả sử b cắt a và c theo thứ tự tại E và F. Chứng minh rằng tứ giác AEFC là một hình thang. d) Chứng minh rằng (EF = AE + CF). Quảng cáo
Đề bài Tứ giác ABCD có hai góc đối diện B và D vuông, hai góc kia không vuông. a) Chứng minh rằng có một đường tròn đi qua bốn điểm A, B, C và D. Ta gọi đó là đường tròn (C). b) Gọi I và K lần lượt là trung điểm của các đường chéo AC và BD của tứ giác. Chứng minh rằng \(IK \bot BD\). c) Kí hiệu các tiếp tuyến của đường tròn (C) tại A, B và C lần lượt là a, b và c. Giả sử b cắt a và c theo thứ tự tại E và F. Chứng minh rằng tứ giác AEFC là một hình thang. d) Chứng minh rằng \(EF = AE + CF\). Phương pháp giải - Xem chi tiết a) Ta có \(\widehat {ABC} + \widehat {ADC} = {90^0} + {90^0} = {180^0}\) nên ABCD là tứ giác nội tiếp b) + AC là đường kính của (C) nên I là tâm của (C). + Suy ra \(ID = IB\). Mà \(KD = KB\) nên IK là đường trung trực của DB. Vậy IK vuông góc với DB. c) Vì \(AC \bot AE\), \(AC \bot CF\) suy ra AE // CF nên AEFC là hình thang. d) Theo tính chất của tiếp tuyến có \(EB = EA,\;BF = FC\) nên \(EF = EB + BF = EA + FC\). Lời giải chi tiết
a) Ta có \(\widehat {ABC} + \widehat {ADC} = {90^0} + {90^0} = {180^0}\) nên ABCD là tứ giác nội tiếp. Do vậy tồn tại đường tròn (C) đi qua bốn điểm A, B, C, D. b) Ta có AC là đường kính của (C) (do AC chắn một cung \(90^\circ \)) nên I là tâm của (C). Từ đó \(ID = IB\), lại có \(KD = KB\) nên IK là đường trung trực của DB. Vậy IK vuông góc với DB. c) Ta có \(AC \bot AE\), \(AC \bot CF\) suy ra AE // CF nên AEFC là hình thang. d) Theo tính chất tiếp tuyến, ta có: \(EB = EA,\;BF = FC.\) Do đó \(EF = EB + BF = EA + FC\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
