Giải bài 1 trang 112 sách bài tập toán 11 - Chân trời sáng tạo tập 1Cho hình chóp S. ABCD có ABCD là hình thang đáy lớn AD. Gọi E, F lần lượt là hai điểm trên hai cạnh SB, SD. a) Tìm giao điểm EF với (SAC). b) Tìm giao điểm BC với (AEF). Quảng cáo
Đề bài Cho hình chóp S. ABCD có ABCD là hình thang đáy lớn AD. Gọi E, F lần lượt là hai điểm trên hai cạnh SB, SD. a) Tìm giao điểm EF với (SAC). b) Tìm giao điểm BC với (AEF). Phương pháp giải - Xem chi tiết Sử dụng kiến thức về giao điểm giữa đường thẳng và mặt phẳng để tìm: Cách tìm giao điểm của đường thẳng d và mặt phẳng \(\left( \alpha \right)\): - Trường hợp 1: Trong mặt phẳng \(\left( \alpha \right)\) có sẵn đường thẳng d’ cắt d tại I: Ta có ngay \(d \cap \left( \alpha \right) = I\) - Trường hợp 2: Trong mặt phẳng \(\left( \alpha \right)\) không có sẵn đường thẳng d’ cắt d. Khi đó ta thực hiện như sau: + Chọn mặt phẳng phụ \(\left( \beta \right)\) chứa d và \(\left( \beta \right)\) cắt \(\left( \alpha \right)\) theo giao tuyến d’. + Gọi \(I = d' \cap d\). Khi đó, \(d \cap \left( \alpha \right) = I\). Lời giải chi tiết
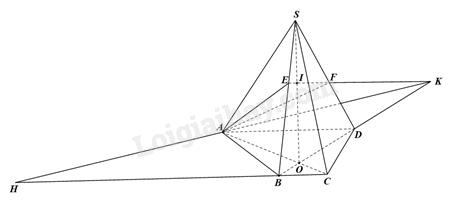
a) Trong mặt phẳng (ABCD), gọi O là giao điểm của AC và BD. Do đó, SO là giao tuyến của mặt phẳng (SAC) và (SBD). Trong mặt phẳng (SBD), gọi I là giao điểm của EF và SO. Vì I thuộc EF, \(I \in SO \subset \left( {SAC} \right)\) nên I là giao điểm của EF và (SAC). b) Trong mặt phẳng (SBD), gọi K là giao điểm của EF và BD. Khi đó, AK là giao tuyến của (ABCD) và (AEF). Trong mặt phẳng (ABCD), gọi H là giao điểm của BC và AK. Vì H thuộc BC, \(H \in AK \subset \left( {AEF} \right)\) nên H là giao điểm của BC và (AEF).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
