Giải bài 1 trang 110, 111 vở thực hành Toán 9 tập 2Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng: a) Tứ giác AEHF nội tiếp đường tròn tâm I; b) ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF. Quảng cáo
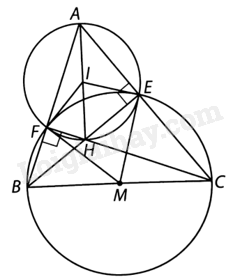
Đề bài Cho tam giác ABC có các đường cao BE, CF cắt nhau tại H. Gọi M là trung điểm của BC và I là trung điểm của AH. Chứng minh rằng: a) Tứ giác AEHF nội tiếp đường tròn tâm I; b) ME, MF tiếp xúc với đường tròn ngoại tiếp tứ giác AEHF. Phương pháp giải - Xem chi tiết a) Chứng minh \(IE = IF = IH = IA\), suy ra tứ giác AEHF nội tiếp đường tròn (I, IA). b) + Chứng minh tứ giác BCEF nội tiếp đường tròn (M, MB). Nên \(\widehat {AEF} = {180^o} - \widehat {FEC} = \widehat {FBC} = \widehat {ABC}\). + Chứng minh \(\widehat {IFA} = \widehat {IAF} = \widehat {HAB} = {90^o} - \widehat {ABC}\), \(\widehat {MFC} = \widehat {FCM}\), suy ra \(\widehat {MFI} = \widehat {MFC} + \widehat {CFI}\) \(= \widehat {MFC} + \left( {{{90}^o} - \widehat {IFA}} \right) \\= \left( {{{90}^o} - \widehat {ABC}} \right) + \widehat {ABC} = {90^o}\) + Do đó, \(MF \bot IF\) nên MF tiếp xúc với (I, IA). + Chứng minh tương tự ta có: ME tiếp xúc với (I, IA). Lời giải chi tiết
a) Do hai tam giác AEH và AFH vuông tại E và F nên \(IE = IF = IH = IA\). Vì vậy tứ giác AEHF nội tiếp đường tròn (I, IA). b) Tương tự như trên, tứ giác BCEF có \(\widehat {BFC} = \widehat {BEC} = {90^o}\) nên tứ giác BCEF nội tiếp đường tròn (M, MB). Suy ra \(\widehat {AEF} = {180^o} - \widehat {FEC} = \widehat {FBC} = \widehat {ABC}\). Vì \(\Delta IFA\) cân tại I nên \(\widehat {IFA} = \widehat {IAF} = \widehat {HAB} = {90^o} - \widehat {ABC}\). (1) Mặt khác, ta có \(MF = MC\), hay \(\Delta MFC\) cân tại M. Suy ra \(\widehat {MFC} = \widehat {FCM}\) (2) Vì vậy ta có: \(\widehat {MFI} = \widehat {MFC} + \widehat {CFI} \\= \widehat {MFC} + \left( {{{90}^o} - \widehat {IFA}} \right) \\= \left( {{{90}^o} - \widehat {ABC}} \right) + \widehat {ABC} \) \(= {90^o}\) (theo (1) và (2)). Do đó, \(MF \bot IF\). Suy ra MF tiếp xúc với (I, IA). Tương tự ME tiếp xúc với (I, IA).
|




















Danh sách bình luận