Giải bài 1 trang 10 sách bài tập toán 11 - Cánh diều

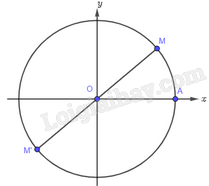
Đề bài

Trên đường tròn lượng giác lấy điểm \(M\) sao cho \(\left( {OA,OM} \right) = {40^o}\). Gọi \(M'\) là điểm đối xứng với \(M\) qua gốc toạ độ. Khi đó số đo của góc lượng giác \(\left( {OA,OM'} \right)\) bằng:

A. \({40^o} + k{360^o}\)                                             

B. \({140^o} + k{360^o}\)

C. \({220^o} + k{360^o}\)                                           

D. \({50^o} + k{360^o}\)

Lời giải chi tiết

Ta có \(\left( {OA,OM} \right) = {40^o}\).

Do \(M'\) đối xứng với \(M\) qua \(O\), ta suy ra \(\left( {OM,OM'} \right) = {180^o}\)

Do đó, \(\left( {OA,OM'} \right) = \left( {OA,OM} \right) + \left( {OM,OM'} \right) + k{360^o} = {220^o} + k{360^o}\)

Đáp án đúng là C.