Đề thi học kì 1 Toán 10 Chân trời sáng tạo - Đề số 13Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... I. Phần trắc nghiệmĐề bài
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Viết mệnh đề sau bằng kí hiệu \(\forall \) hoặc \(\exists \): “Có một số nguyên bằng bình phương của chính nó”.
Câu 2 :
Cho tập hợp \(A = \{ x \in \mathbb{R}| - 3 < x < 1\} \). Tập A là tập nào sau đây?
Câu 3 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Câu 4 :
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - 5y - 1 > 0\\2x + y + 5 > 0\\x + y + 1 < 0\end{array} \right.\)?
Câu 5 :
Cho tam giác ABC có \(A = {120^o}\) thì đẳng thức nào sau đây đúng?
Câu 6 :
Cho tam giác ABC. Tìm công thức đúng trong các công thức sau:
Câu 7 :
Cho hình bình hành ABCD. Vecto nào sau đây cùng phương với \(\overrightarrow {AB} \)?
Câu 8 :
Biết \(\overrightarrow {AB} = \overrightarrow a \). Gọi C là điểm thỏa mãn \(\overrightarrow {CA} = \overrightarrow {AB} \). Chọn khẳng định đúng.
Câu 9 :
Tập xác định của hàm số \(y = \sqrt {x + 2} - \sqrt {x + 3} \) là
Câu 10 :
Cho hai vecto \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \), \(\alpha \) là góc tạo vởi hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\). Chọn khẳng định đúng.
Câu 11 :
Quy tròn số 12,4567 đến hàng phần trăm ta được
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
a) a > 0.
Đúng
Sai
b) c > 0.
Đúng
Sai
c) a – 2b + c = 7.
Đúng
Sai
d) \(a - {b^2} + {c^3} = 10\).
Đúng
Sai
Câu 2 :
Cho \(\sin \alpha = \frac{1}{2}\) với \({0^o} < \alpha < {90^o}\). a) \(\cos \alpha < 0\).
Đúng
Sai
b) \({\cos ^2}\alpha = \frac{5}{9}\).
Đúng
Sai
c) \(\cos ({180^o} - \alpha ) = - \frac{1}{3}\).
Đúng
Sai
d) Giá trị biểu thức \(P = \frac{{\sin \alpha + \cos \alpha }}{{2\sin \alpha + \cos \alpha }} = \frac{{1 + 2\sqrt 2 }}{{2 + 2\sqrt 2 }}\).
Đúng
Sai
Câu 3 :
Cho tam giác ABC có G là trọng tâm. Gọi D là điểm đối xứng của B qua G và M là trung điểm của BC. a) \(\overrightarrow {MG} = \overrightarrow {MG} + \overrightarrow {GD} \).
Đúng
Sai
b) \(\overrightarrow {AG} = 2\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
Đúng
Sai
c) \(\overrightarrow {CD} = \overrightarrow {AB} - \overrightarrow {AC} + \frac{1}{3}\overrightarrow {BG} \).
Đúng
Sai
d) \(\overrightarrow {MD} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
Đúng
Sai
Câu 4 :
Cho mẫu số liệu thống kê số giờ học thêm của 10 học sinh trong một tuần: 2, 3, 4, 4, 5, 6, 6, 7, 8, 15. a) Số giờ học thêm trung bình của 10 học sinh trên là 6 giờ.
Đúng
Sai
b) Mốt của mẫu số liệu trên bằng 15.
Đúng
Sai
c) Giá trị ngoại lệ của mẫu số liệu trên là 2.
Đúng
Sai
d) Độ lệch chuẩn về số giờ học thêm của 10 học sinh trên là \(\sqrt {12} \) giờ.
Đúng
Sai
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Cho hai tập hợp khác rỗng A = [0;5]; B = (2m;3m+1] đều khác tập rỗng. Có bao nhiêu giá trị nguyên m để \(A \cap B \ne \emptyset \)? Đáp án:
Câu 2 :
Một người thợ mộc làm những cái bàn và những cái ghế. Mỗi cái bàn khi bán lãi 150 nghìn đồng, Đáp án:
Câu 3 :
Muốn đo chiều cao CD của một cái tháp mà ta không thể đến được tâm C của chân tháp. Trong mặt phẳng đứng chứa chiều cao CD của tháp ta chọn hai điểm A và B sao cho ba điểm A, B, C thẳng hàng. Giả sử ta đo được khoảng cách AB = 24 m và các góc \(\widehat {CAD} = {63^o}\), \(\widehat {CBD} = {48^o}\). Hãy tính chiều cao h = CD của tháp (kết quả làm tròn đến hàng phần mười).
Đáp án:
Câu 4 :
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều bằng 100 N và góc \(\widehat {AMB} = {90^o}\). Tính cường độ của lực \(\overrightarrow {{F_3}} \) (làm tròn đến hàng đơn vị).
Đáp án:
Câu 5 :
Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ.
Biết chiều cao cổng parabol là 4 m, cửa chính (ở giữa parabol) cao 3 m và rộng 4 m. Tính khoảng cách giữa hai chân cổng parabol ấy (đoạn AB như hình vẽ). Đáp án:
Câu 6 :
Mẫu số liệu sau đây cho biết sĩ số của 5 lớp khối 10 tại một trường trung học phổ thông. 43 45 46 41 40 Tìm phương sai của mẫu số liệu trên. Đáp án: Lời giải và đáp án
Phần I: Câu trắc nghiệm nhiều phương án lựa chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 :
Viết mệnh đề sau bằng kí hiệu \(\forall \) hoặc \(\exists \): “Có một số nguyên bằng bình phương của chính nó”.
Đáp án : D Phương pháp giải :
Đọc kĩ mệnh đề và áp dụng quy tắc sử dụng kí hiệu \(\forall \) và \(\exists \). Lời giải chi tiết :
“Có một số nguyên” tức là tồn tại số nguyên: \(\exists x \in \mathbb{Z}\). “Số (nguyên) bằng bình phương của chính nó”: \(x = {x^2}\). Vậy mệnh đề đúng là “\(\exists x \in \mathbb{Z},x = {x^2}\)”.
Câu 2 :
Cho tập hợp \(A = \{ x \in \mathbb{R}| - 3 < x < 1\} \). Tập A là tập nào sau đây?
Đáp án : D Phương pháp giải :
Với dấu “>” hoặc “<” ta dùng kí hiệu khoảng (). Lời giải chi tiết :
\(x \in \mathbb{R}\) nên mọi số thực thỏa mãn -3 < x < 1 đều thuộc A. Tập {-3;1} chỉ có 2 giá trị nên A sai. Với dấu “>” hoặc “<” ta dùng kí hiệu khoảng. Trong trường hợp này dùng kí hiệu nửa khoảng ở cả hai đầu mút. Vậy A = (-3;1).
Câu 3 :
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
Đáp án : A Phương pháp giải :
Quan sát dạng (ẩn, bậc) của bất phương trình. Lời giải chi tiết :
Các bất phương trình ở đáp án B, C, D đều là bất phương trình bậc hai hai ẩn.
Câu 4 :
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - 5y - 1 > 0\\2x + y + 5 > 0\\x + y + 1 < 0\end{array} \right.\)?
Đáp án : C Phương pháp giải :
Thay tọa độ các điểm vào hệ phương trình, nếu thỏa mãn hệ điểm đó thuộc miền nghiệm. Lời giải chi tiết :
Thay tọa độ các điểm vào hệ, chỉ có điểm (0;-2) thỏa mãn hệ.
Câu 5 :
Cho tam giác ABC có \(A = {120^o}\) thì đẳng thức nào sau đây đúng?
Đáp án : B Phương pháp giải :
Sử dụng định lí Cosin cho tam giác. Lời giải chi tiết :
\({a^2} = {b^2} + {c^2} - 2bc\cos A = {b^2} + {c^2} - 2bc\cos {120^o} = {b^2} + {c^2} - 2bc.\left( { - \frac{1}{2}} \right) = {b^2} + {c^2} + bc\).
Câu 6 :
Cho tam giác ABC. Tìm công thức đúng trong các công thức sau:
Đáp án : A Phương pháp giải :
Áp dụng công thức tính diện tích tam giác. Lời giải chi tiết :
\(S = \frac{1}{2}bc\sin A\).
Câu 7 :
Cho hình bình hành ABCD. Vecto nào sau đây cùng phương với \(\overrightarrow {AB} \)?
Đáp án : A Phương pháp giải :
Các vecto cùng phương có giá song song với nhau. Lời giải chi tiết :
Vì ABCD là hình bình hành nên AB // CD. Khi đó \(\overrightarrow {AB} = \overrightarrow {BA} \), \(\overrightarrow {AB} = \overrightarrow {CD} \) và \(\overrightarrow {AB} = \overrightarrow {DC} \).
Câu 8 :
Biết \(\overrightarrow {AB} = \overrightarrow a \). Gọi C là điểm thỏa mãn \(\overrightarrow {CA} = \overrightarrow {AB} \). Chọn khẳng định đúng.
Đáp án : C Phương pháp giải :
Dựng hình thỏa mãn đẳng thức trên và nhận xét. Lời giải chi tiết :
Vì \(\overrightarrow {CA} = \overrightarrow {AB} \) nên hai vecto trên cùng phương và \(\overrightarrow {CA} ,\overrightarrow {AB} \) cùng chiều.
Khi đó A, B, C thẳng hàng và A nằm giữa B, C. Vậy khẳng định đúng là \(\overrightarrow {CB} = 2\overrightarrow a \).
Câu 9 :
Tập xác định của hàm số \(y = \sqrt {x + 2} - \sqrt {x + 3} \) là
Đáp án : B Phương pháp giải :
Biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0. Lời giải chi tiết :
Để hàm số trên xác định thì \(\left\{ \begin{array}{l}x + 2 \ge 0\\x + 3 \ge 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x \ge - 2\\x \ge - 3\end{array} \right.\) Vậy \(D = [ - 2; + \infty )\).
Câu 10 :
Cho hai vecto \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \), \(\alpha \) là góc tạo vởi hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\). Chọn khẳng định đúng.
Đáp án : A Phương pháp giải :
Áp dụng công thức tính tích vô hướng: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\). Lời giải chi tiết :
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\) \( \Rightarrow - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right| = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \alpha \) \( \Rightarrow \cos \alpha = - 1\) \( \Rightarrow \alpha = {180^o}\).
Câu 11 :
Quy tròn số 12,4567 đến hàng phần trăm ta được
Đáp án : B Phương pháp giải :
Quy tròn đến hàng phần trăm là quy tròn đến chữ số thập phân thứ hai. Lời giải chi tiết :
Xét chữ số thập phân thứ ba là 6 > 5 nên số sau khi quy tròn là 12,46.
Đáp án : D Phương pháp giải :
Xác định khoảng biến thiên bằng cách lấy giá trị lớn nhất trừ đi giá trị nhỏ nhất. Lời giải chi tiết :
Giá trị nhỏ nhất của mẫu số liệu là 38. Giá trị lớn nhất của mẫu số liệu là 60. Khoảng biến thiên của mẫu số liệu là R = 60 – 38 = 22.
Phần II: Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
a) a > 0.
Đúng
Sai
b) c > 0.
Đúng
Sai
c) a – 2b + c = 7.
Đúng
Sai
d) \(a - {b^2} + {c^3} = 10\).
Đúng
Sai
Đáp án
a) a > 0.
Đúng
Sai
b) c > 0.
Đúng
Sai
c) a – 2b + c = 7.
Đúng
Sai
d) \(a - {b^2} + {c^3} = 10\).
Đúng
Sai
Phương pháp giải :
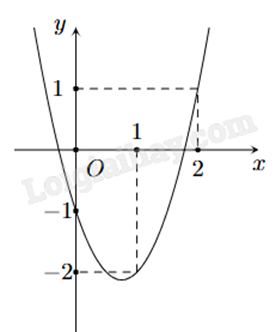
Quan sát đồ thị và nhận xét. Tìm hệ số a, b, c bằng cách thay tọa độ các điểm vào hàm số và giải hệ. Lời giải chi tiết :
a) Đúng. Vì đồ thị hướng bề lõm lên trên nên a > 0. b) Sai. Vì đồ thị cắt trục tung tại điểm có tung độ y = -1 < 0 nên c = -1 < 0. c) Sai. Vì đồ thị đi qua điểm có tọa độ (2;1) và (1;-2) nên ta có: \(\left\{ \begin{array}{l}a{.2^2} + b.2 + ( - 1) = 1\\a{.1^2} + b.1 + ( - 1) = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4a + 2b = 1\\a + b = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{3}{2}\\b = - \frac{5}{2}\end{array} \right.\) Vậy \(a - 2b + c = \frac{3}{2} - 2\left( { - \frac{5}{2}} \right) + ( - 1) = \frac{{11}}{2}\). d) Sai. \(a - {b^2} + {c^3} = \frac{3}{2} - {\left( { - \frac{5}{2}} \right)^2} + {( - 1)^3} = - \frac{{23}}{4}\).
Câu 2 :
Cho \(\sin \alpha = \frac{1}{2}\) với \({0^o} < \alpha < {90^o}\). a) \(\cos \alpha < 0\).
Đúng
Sai
b) \({\cos ^2}\alpha = \frac{5}{9}\).
Đúng
Sai
c) \(\cos ({180^o} - \alpha ) = - \frac{1}{3}\).
Đúng
Sai
d) Giá trị biểu thức \(P = \frac{{\sin \alpha + \cos \alpha }}{{2\sin \alpha + \cos \alpha }} = \frac{{1 + 2\sqrt 2 }}{{2 + 2\sqrt 2 }}\).
Đúng
Sai
Đáp án
a) \(\cos \alpha < 0\).
Đúng
Sai
b) \({\cos ^2}\alpha = \frac{5}{9}\).
Đúng
Sai
c) \(\cos ({180^o} - \alpha ) = - \frac{1}{3}\).
Đúng
Sai
d) Giá trị biểu thức \(P = \frac{{\sin \alpha + \cos \alpha }}{{2\sin \alpha + \cos \alpha }} = \frac{{1 + 2\sqrt 2 }}{{2 + 2\sqrt 2 }}\).
Đúng
Sai
Phương pháp giải :
Sử dụng kiến thức về dấu của các giá trị lượng giác của các góc. Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\), \(\cos ({180^o} - \alpha ) = - \cos \alpha \). Lời giải chi tiết :
a) Sai. Có \({0^o} < \alpha < {90^o}\) suy ra \(\cos \alpha > 0\). b) Sai. \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( {\frac{1}{3}} \right)^2} = \frac{8}{9}\). c) Sai. Vì \(\cos \alpha > 0\) nên \(\cos \alpha = \sqrt {\frac{8}{9}} = \frac{{2\sqrt 2 }}{3}\). \(\cos ({180^o} - \alpha ) = - \cos \alpha = - \frac{{2\sqrt 2 }}{3}\). d) Đúng. Ta có: \(P = \frac{{\sin \alpha + \cos \alpha }}{{2\sin \alpha + \cos \alpha }} = \frac{{\frac{1}{3} + \frac{{2\sqrt 2 }}{3}}}{{2.\frac{1}{3} + \frac{{2\sqrt 2 }}{3}}} = \frac{{1 + 2\sqrt 2 }}{{2 + 2\sqrt 2 }}\).
Câu 3 :
Cho tam giác ABC có G là trọng tâm. Gọi D là điểm đối xứng của B qua G và M là trung điểm của BC. a) \(\overrightarrow {MG} = \overrightarrow {MG} + \overrightarrow {GD} \).
Đúng
Sai
b) \(\overrightarrow {AG} = 2\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
Đúng
Sai
c) \(\overrightarrow {CD} = \overrightarrow {AB} - \overrightarrow {AC} + \frac{1}{3}\overrightarrow {BG} \).
Đúng
Sai
d) \(\overrightarrow {MD} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
Đúng
Sai
Đáp án
a) \(\overrightarrow {MG} = \overrightarrow {MG} + \overrightarrow {GD} \).
Đúng
Sai
b) \(\overrightarrow {AG} = 2\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
Đúng
Sai
c) \(\overrightarrow {CD} = \overrightarrow {AB} - \overrightarrow {AC} + \frac{1}{3}\overrightarrow {BG} \).
Đúng
Sai
d) \(\overrightarrow {MD} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
Đúng
Sai
Phương pháp giải :
Áp dụng quy tắc ba điểm, quy tắc hình bình hành, tính chất trung điểm đối với vecto, quy tắc cộng, trừ hai vecto. Lời giải chi tiết :
a) Đúng. Theo quy tắc ba điểm: \(\overrightarrow {MG} = \overrightarrow {MG} + \overrightarrow {GD} \). b) Sai. \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \). c) Sai. \(\overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {BD} = \overrightarrow {AB} - \overrightarrow {AC} + 2\overrightarrow {BG} \). d) Đúng. \(\overrightarrow {MD} = \overrightarrow {MG} + \overrightarrow {GD} = - \frac{1}{3}\overrightarrow {AM} + \overrightarrow {BG} = - \frac{1}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + \left( {\overrightarrow {BA} + \frac{2}{3}\overrightarrow {AM} } \right)\) \( = - \frac{1}{6}\overrightarrow {AB} - \frac{1}{6}\overrightarrow {AC} - \overrightarrow {AB} + \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
Câu 4 :
Cho mẫu số liệu thống kê số giờ học thêm của 10 học sinh trong một tuần: 2, 3, 4, 4, 5, 6, 6, 7, 8, 15. a) Số giờ học thêm trung bình của 10 học sinh trên là 6 giờ.
Đúng
Sai
b) Mốt của mẫu số liệu trên bằng 15.
Đúng
Sai
c) Giá trị ngoại lệ của mẫu số liệu trên là 2.
Đúng
Sai
d) Độ lệch chuẩn về số giờ học thêm của 10 học sinh trên là \(\sqrt {12} \) giờ.
Đúng
Sai
Đáp án
a) Số giờ học thêm trung bình của 10 học sinh trên là 6 giờ.
Đúng
Sai
b) Mốt của mẫu số liệu trên bằng 15.
Đúng
Sai
c) Giá trị ngoại lệ của mẫu số liệu trên là 2.
Đúng
Sai
d) Độ lệch chuẩn về số giờ học thêm của 10 học sinh trên là \(\sqrt {12} \) giờ.
Đúng
Sai
Phương pháp giải :
a) Sử dụng công thức tính số trung bình. b) Mốt của mẫu số liệu là giá trị xuất hiện nhiều nhất. c) Giá trị ngoại lệ nằm ngoài đoạn \([{Q_1} - 1,5{\Delta _Q};{Q_3} + 1,5{\Delta _Q}]\). d) Sử dụng công thức tính độ lệch chuẩn. Lời giải chi tiết :
a) Đúng. Số giờ học thêm trung bình của 10 học sinh là \(\overline x = \frac{{2.1 + 3.1 + 4.2 + 5.1 + 6.2 + 7.1 + 8.1 + 15.1}}{{1 + 1 + 2 + 1 + 2 + 1 + 1 + 1}} = 6\) (giờ). b) Sai. Mốt của mẫu số liệu trên là 4 và 6 vì có tần số lớn nhất (bằng 2). c) Sai. Trung vị là \({Q_2} = \frac{{5 + 6}}{2} = 10,5\). Tứ phân vị thứ nhất là \({Q_1} = 4\), tứ phân vị thứ ba là \({Q_3} = 7\). Khoảng tứ phân vị là \({\Delta _Q} = {Q_3} - {Q_1} = 7 - 4 = 3\). Giá trị ngoại lệ sẽ nhỏ hơn \({Q_1} - 1,5{\Delta _Q} = 4 - 1,5.3 = - 0,5\) và lớn hơn \({Q_3} + 1,5{\Delta _Q} = 7 + 1,5.3 = 11,5\). Vậy 15 là giá trị ngoại lệ. d) Đúng. Phương sai của mẫu số liệu: \({s^2} = \frac{1}{{10}}\left[ {{{\left( {2 - 6} \right)}^2} + {{\left( {3 - 6} \right)}^2} + 2.{{\left( {4 - 6} \right)}^2} + {{\left( {5 - 6} \right)}^2} + 2.{{\left( {6 - 6} \right)}^2} + {{\left( {7 - 6} \right)}^2} + {{\left( {8 - 6} \right)}^2} + {{\left( {15 - 6} \right)}^2}} \right] = 12\) Độ lệch chuẩn của mẫu số liệu là \(\sqrt {{s^2}} = \sqrt {12} \).
Phần III: Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1 :
Cho hai tập hợp khác rỗng A = [0;5]; B = (2m;3m+1] đều khác tập rỗng. Có bao nhiêu giá trị nguyên m để \(A \cap B \ne \emptyset \)? Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tìm điều kiện để \(A \cap B = \emptyset \), từ đó suy ra điều kiện để \(A \cap B \ne \emptyset \) bằng cách lấy phần bù. Lời giải chi tiết :
\(B \ne \emptyset \) khi \(2m < 3m + 1 \Rightarrow m > - 1\). Ta có \(A \cap B = \emptyset \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}2m \ge 5\\3m + 1 < 0\end{array} \right.\\m > - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \ge \frac{5}{2}\\ - 1 < m < - \frac{1}{3}\end{array} \right.\) Suy ra \(A \cap B \ne \emptyset \Leftrightarrow m \in \left[ { - \frac{1}{3};\frac{5}{2}} \right)\). Các giá trị nguyên m thỏa mãn là 0; 1; 2. Vậy có 3 giá trị nguyên m thỏa mãn yêu cầu đề bài.
Câu 2 :
Một người thợ mộc làm những cái bàn và những cái ghế. Mỗi cái bàn khi bán lãi 150 nghìn đồng, Đáp án: Đáp án
Đáp án: Phương pháp giải :
Ứng dụng hệ bất phương trình bậc nhất hai ẩn. Lời giải chi tiết :
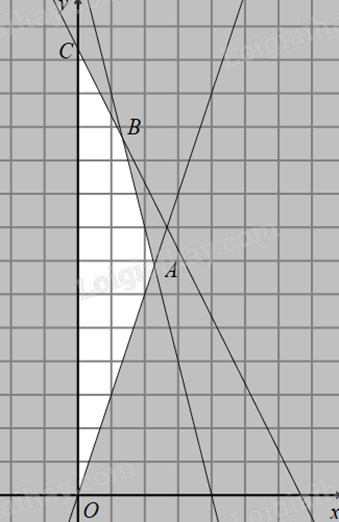
Gọi x và y lần lượt là số bàn và số ghế mà người thợ mộc sản xuất trong một tuần \((x,y \ge 0)\). Để làm x cái bàn cần 6x (giờ), làm y cái ghế cần 3y (giờ). Người thợ mộc chỉ có thể làm 40 giờ/tuần nên \(6x + 3y \le 40\). Số ghế gấp ít nhất ba lần số bàn nên \(y \ge 3x\). Một cái bàn chiếm chỗ bằng 4 cái ghế và ta có phòng để được nhiều nhất 4 cái bàn/tuần nên \(x + \frac{4}{y} \le 4\). Ta có hệ bất phương trình \(\left\{ \begin{array}{l}6x + 3y \le 40\\y \ge 3x\\x + \frac{y}{4} \le 4\\x,y \ge 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}6x + 3y \le 40\\y \ge 3x\\4x + y \le 16\\x,y \ge 0\end{array} \right.\) (*). Lợi nhuận thu được là f(x;y) = 150x + 50y (nghìn đồng). Bài toán trở thành tìm giá trị lớn nhất của f(x;y) trên miền nghiệm của hệ (*).
Miền nghiệm của hệ (*) là miền tứ giác OABC (kể cả biên) với \(A\left( {\frac{{16}}{7};\frac{{48}}{7}} \right)\), \(B\left( {\frac{4}{3};\frac{{32}}{2}} \right)\), \(C\left( {0;\frac{{40}}{3}} \right)\). Thay tọa độ các điểm trên vào f(x;y) thấy \(f\left( {\frac{4}{3};\frac{{32}}{3}} \right) = \frac{{2200}}{3}\) là giá trị lớn nhất. Như vậy người thợ này cần sản xuất 4 cái bàn và 32 cái ghế trong vòng 3 tuần để thu về số tiên lãi lớn nhất. Ta có a + b + c = 4 + 32 + 3 = 39.
Câu 3 :
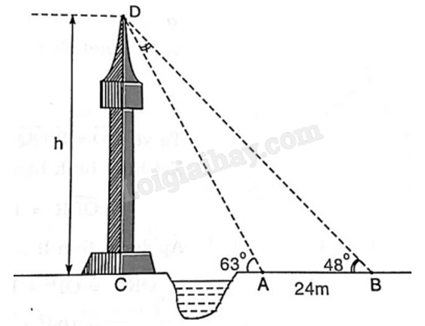
Muốn đo chiều cao CD của một cái tháp mà ta không thể đến được tâm C của chân tháp. Trong mặt phẳng đứng chứa chiều cao CD của tháp ta chọn hai điểm A và B sao cho ba điểm A, B, C thẳng hàng. Giả sử ta đo được khoảng cách AB = 24 m và các góc \(\widehat {CAD} = {63^o}\), \(\widehat {CBD} = {48^o}\). Hãy tính chiều cao h = CD của tháp (kết quả làm tròn đến hàng phần mười).
Đáp án: Đáp án
Đáp án: Phương pháp giải :
B1: Tính các góc của tam giác ABD. B2: Tính AD bằng định lí Sin cho tam giác ABD. B3: Sử dụng hệ thức lượng trong tam giác vuông CAD để tính CD. Lời giải chi tiết :
+) \(\widehat {CAD} + \widehat {BAD} = {180^o} \Rightarrow \widehat {BAD} = {180^o} - \widehat {CAD} = {180^o} - {63^o} = {117^o}\). +) Xét tam giác ABD có \(\widehat D = {180^o} - \widehat A - \widehat B = {180^o} - {117^o} - {48^o} = {15^o}\). Áp dụng định lí Sin cho tam giác ABD: \(\frac{{AB}}{{\sin \widehat {BDA}}} = \frac{{AD}}{{\sin \widehat {ABD}}}\). Suy ra \(AD = \frac{{AB\sin \widehat {ABD}}}{{\sin \widehat {ADB}}} = \frac{{24\sin {{48}^o}}}{{\sin {{15}^o}}}\). Xét tam giác ACD vuông tại C: \(\sin \widehat {CAD} = \frac{{CD}}{{AD}}\). Suy ra \(CD = AD\sin \widehat {CAD} = \frac{{24\sin {{48}^o}}}{{\sin {{15}^o}}}\sin {63^o} \approx 61,4\) (m).
Câu 4 :
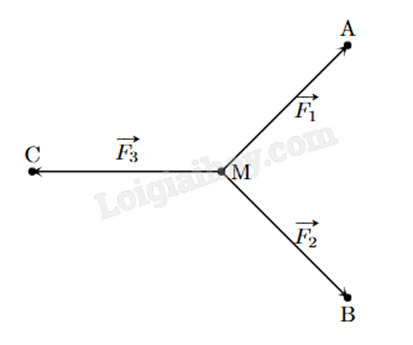
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều bằng 100 N và góc \(\widehat {AMB} = {90^o}\). Tính cường độ của lực \(\overrightarrow {{F_3}} \) (làm tròn đến hàng đơn vị).
Đáp án: Đáp án
Đáp án: Phương pháp giải :
Sử dụng quy tắc tổng hợp lực, quy tắc hình bình hành. Lời giải chi tiết :
Dựng hình bình hành AMBD. Vì \(\widehat {AMB} = {90^o}\) nên AMBD là hình vuông. Áp dụng quy tắc hình bình hành, ta có \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MD} \). Vì vật đứng yên nên \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \). Từ đó ta suy ra \(\overrightarrow {MD} + \overrightarrow {MC} = \overrightarrow 0 \) hay \(\overrightarrow {MD} = - \overrightarrow {MC} \). Khi đó \(\left| {\overrightarrow {MD} } \right| = \left| { - \overrightarrow {MC} } \right|\) tức MD = MC. Vì MD là đường chéo của hình vuông cạnh 100 nên \(MD = 100\sqrt 2 \). Vậy \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MC} } \right| = 100\sqrt 2 \approx 141\) N.
Câu 5 :
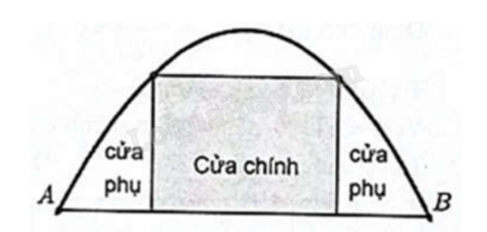
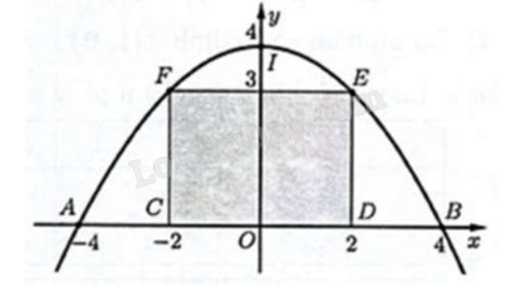
Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ.
Biết chiều cao cổng parabol là 4 m, cửa chính (ở giữa parabol) cao 3 m và rộng 4 m. Tính khoảng cách giữa hai chân cổng parabol ấy (đoạn AB như hình vẽ). Đáp án: Đáp án
Đáp án: Phương pháp giải :
Dựng hệ trục Oxy một cách phù hợp. Thay tọa độ các điểm thuộc parabol vào hàm số \(y = a{x^2} + bx + c\) rồi tính hệ số a, b, c. Tìm giao điểm của parabol với trục Ox và tính khoảng cách giữa hai giao điểm đó. Lời giải chi tiết :
Dựng hệ trục Oxy như hình vẽ.
Gọi (P): \(y = a{x^2} + bx + c\) \((a \ne 0)\). Ta có (P) đi qua các điểm I(0;4), E(2;3), F(-2;3) nên \(\left\{ \begin{array}{l}c = 4\\4a + 2b + c = 3\\4a - 2b + c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{4}\\b = 0\\c = 4\end{array} \right.\). Từ đó suy ra (P): \(y = - \frac{1}{4}{x^2} + 4\). Hai điểm A, B là giao điểm của (P) với trục Ox nên hoành độ thỏa mãn \( - \frac{1}{4}{x^2} + 4 = 0 \Leftrightarrow x = \pm 4\). Do đó A(-4;0) và B(4;0). Suy ra AB = 8.
Câu 6 :
Mẫu số liệu sau đây cho biết sĩ số của 5 lớp khối 10 tại một trường trung học phổ thông. 43 45 46 41 40 Tìm phương sai của mẫu số liệu trên. Đáp án: Đáp án
Đáp án: Phương pháp giải :
Tính phương sai dựa vào công thức. Lời giải chi tiết :
Số học sinh trung bình các lớp khối 10 là \(\overline x = \frac{{43 + 45 + 46 + 41 + 40}}{5} = 43\). Phương sai của mẫu số liệu là: \({s^2} = \frac{1}{5}\left[ {{{\left( {43 - 43} \right)}^2} + {{\left( {45 - 43} \right)}^2} + {{\left( {46 - 43} \right)}^2} + {{\left( {41 - 43} \right)}^2} + {{\left( {40 - 43} \right)}^2}} \right] = 5,2\).
|
