Đề thi giữa học kì 1 Vật lí 10 Kết nối tri thức - Đề số 7Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề thi giữa học kì 1 - Đề số 7Đề bài
PHẦN I. CÂU TRẮC NGHIỆM PHƯƠNG ÁN NHIỀU LỰA CHỌN.
Câu 1 :
Đơn vị đo khối lượng trong hệ thống đo lường SI là
Câu 2 :
Để đo trọng lực tác dụng lên vật m, chỉ cần dùng dụng cụ đo là
Câu 4 :
Độ dịch chuyển và quãng đường đi được của vật có độ lớn bằng nhau khi vật
Câu 5 :
Một con kiến bò quanh miệng của một cái bát được đúng 1 vòng. Đường kính của miệng chén là 6 cm. Độ dịch chuyển của con kiến là
Câu 6 :
Một con kiến bò quanh miệng của một cái bát được đúng 1 vòng. Đường kính của miệng chén là 6 cm. Độ dịch chuyển của con kiến là
Câu 7 :
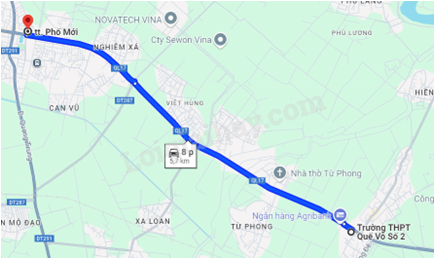
Một người sử dụng google map để tra đường đi từ Trường THPT Quế võ số 2 đến ngã tư Phố mới thuộc thành phố Bắc Ninh được kết quả như hình vẽ bên dưới. Để đúng như bản đồ gợi ý, quãng đường dài 5,7 km, thời gian đi là 8 phút thì người đó phải di với tốc độ trung bình bằng
Câu 8 :
Trong hệ tọa độ vOt, với Ov là trục vận tốc và Ot là trục thời gian. Đồ thị vận tốc theo thời gian của chuyển động thẳng đều là
Câu 9 :
Người ngồi trên tàu A đang đi vào ga thấy cây bên đường và tàu B đang chuyển động giống nhau với cùng vận tốc. Vậy xe B và xe A có tính chất chuyển động thế nào?
Câu 10 :
Đơn vị của gia tốc là
Câu 11 :
Câu nào sai? Trong chuyển động thẳng nhanh dần đều thì
Câu 12 :
Quá trình xe máy tăng tốc khi bắt đầu di chuyển và quá trình xe máy giảm tốc khi muốn dừng lại trong thời gian ngắn lần lượt tương ứng với chuyển động
Câu 13 :
Rơi tự do là chuyển động
Câu 14 :
Một vật rơi tự do từ một độ cao \(h.\) Biết rằng trong giây cuối cùng vật rơi được quãng đường \(25\,m.\) Lấy \(g = 10\,m{\rm{/}}{s^2}.\) Thời gian rơi của vật là
Câu 15 :
Một tàu vũ trụ đang di chuyển qua bề mặt của một tiểu hành tinh có khối lượng rất nhỏ. Tàu thả rơi một mẫu vật từ độ cao 50 m so với bề mặt của tiểu hành tinh. Gia tốc trọng trường trên tiểu hành tinh là g = 0,3 m/s2. Mẫu vật chạm bề mặt hành tinh sau
Câu 16 :
Một cầu thủ bóng đá thực hiện cú ném biên với vận tốc ban đầu là 10 m/s ở độ cao 2 m so với mặt đất. Lấy g = 9,8 m/s2, bỏ qua lực cản của không khí, khoảng cách mà quả bóng sẽ rơi xuống đất theo phương ngang tính từ vị trí ném là
Câu 17 :
Để xác định vi phạm về tốc độ của các phương tiện giao thông đang di chuyển trên các tuyến đường, cảnh sát giao thông sử dụng
Câu 18 :
Một vật được thả từ độ cao 1,6 m trên mặt trăng, nơi gia tốc trong trường là g ≈ 1,6 m/s2. Một nhà khoa học đo thời gian vật rơi và thu được kết quả là 1,1 s. Dựa trên kết quả tính toán gia tốc thực nghiệm và so sánh với gia tốc lí thuyết, kết luận nào sau đây là đúng?
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI.
Câu 1 :
Trong thí nghiệm đo gia tốc rơi tự do tại nơi có gia tốc rơi tự do g = 9,8 m/s2, bạn thực hiện 5 lần thí nghiệm và ghi lại thời gian rơi của vật thể. Biết sai số lấy một vạch chia nhỏ nhất. Bảng kết quả được ghi lại như sau
a) Chuyển động rơi tự do là chuyển động thẳng nhanh dần đều với gia tốc g.
Đúng
Sai
b) Kết quả đo thời gian \(\bar t\)= 1,44 (s).
Đúng
Sai
c) Kết quả giá trị trung bình của gia tốc rơi tự do vào khoảng: 9,6 m/s2
Đúng
Sai
d) Giá trị thực nghiệm khác giá trị lí thuyết là chủ yếu do sai số dụng cụ khi thực hiện phép đo thời gian.
Đúng
Sai
Câu 2 :
Một vận động viên bơi về phía Bắc với vận tốc 1,7 m/s. Nước sông chảy với vận tốc 1 m/s về phía Đông. Thời gian bơi của vận động viên là 15 phút. a) Vận động viên bơi đến bờ bên kia sẽ bị lệch về phía Đông so với điểm xuất phát
Đúng
Sai
b) Vận tốc của vận động viên so với bờ vào khoảng 1,97 m/s
Đúng
Sai
c) Để bơi đến đúng điểm đích thì vận động viên phải xuất phát từ điểm cách điểm đích theo phía Đông khoảng 0,25 m
Đúng
Sai
d) Để tiết kiệm sức nhất, vận động viên nên bơi ngược chiều dòng nước
Đúng
Sai
Câu 3 :
Từ độ cao \(h = 1,6(m)\), người ta ném một quả bóng theo phương ngang với vận tốc ban đầu \({{\rm{v}}_{\rm{0}}}{\rm{ = 20 m/s}}\) vào một chiếc rổ. Lấy \({\rm{g = 10 m/}}{{\rm{s}}^{\rm{2}}}{\rm{.}}\) a) Theo phương ngang, vật chuyển động thẳng đều với vận tốc 20 m/s.
Đúng
Sai
b) Quỹ đạo chuyển động của quả bóng được nhìn thấy có dạng là đường thẳng.
Đúng
Sai
c) Thời gian rơi của vật lớn hơn thời gian rơi của vật nếu thả rơi từ đúng điểm ném
Đúng
Sai
d) Để vật rơi trúng rổ thì rổ phải đặt cách điểm ném theo phương ngang một đoạn 8\(\sqrt 2 \)m.
Đúng
Sai
Câu 4 :
Một ô tô đang chạy với tốc độ \(54\;{\rm{km/h}}\) trên đoạn đường thẳng thì người lái xe hãm phanh cho ô tô chạy thẳng chậm dần đều để vào chỗ đỗ xe. Sau khi chạy thêm \(250\;{\rm{m}}\) thì tốc độ của ô tô chỉ còn \(5\;\;{\rm{m/s}}{\rm{.}}\) Biết chỗ xe cách người 300 m. a) Độ dịch chuyển của điện thoại khi chạm đất là d = 250 m.
Đúng
Sai
b) Ô tô từ khi hãm phan chuyển động với gia tốc có độ lớn 0,4 m/s2.
Đúng
Sai
c) Thời gian ô tô chạy thêm 250 m kể từ khi hãm phanh là 20 s.
Đúng
Sai
d) Ô tô dừng lại trước khi đến chỗ cần đỗ xe
Đúng
Sai
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN.
Câu 2 :
Trong một lần thử xe ô tô, người ta xác định được độ dịch chuyển của xe theo thời gian như bảng sau.
Biết xe chuyển động thẳng theo một chiều nhất định. Vận tốc trung bình của ô tô trong 3 giây đầu tiên, trong 3 giây cuối cùng lần lượt là\({v_1},{v_2}\). Tổng \(\left( {{v_1} + 2{v_2}} \right)\) bằng bao nhiêu m/s? (Kết quả lấy đến phần nguyên). Lời giải và đáp án
PHẦN I. CÂU TRẮC NGHIỆM PHƯƠNG ÁN NHIỀU LỰA CHỌN.
Câu 1 :
Đơn vị đo khối lượng trong hệ thống đo lường SI là
Đáp án : C Phương pháp giải :
Vận dụng kiến thức về đo khối lượng Lời giải chi tiết :
Đơn vị đo khối lượng trong hệ thống đo lường SI là kilôgam Đáp án: C
Câu 2 :
Để đo trọng lực tác dụng lên vật m, chỉ cần dùng dụng cụ đo là
Đáp án : A Phương pháp giải :
Vận dụng kiến thức về đo trọng lực Lời giải chi tiết :
Để đo trọng lực tác dụng lên vật m, chỉ cần dùng dụng cụ đo là lực kế Đáp án: A
Đáp án : A Phương pháp giải :
Vận dụng kiến thức về phương pháp thực nghiệm Lời giải chi tiết :
Để xác định thể tích của một hình lập phương bằng phương pháp thực nghiệm ta cần dùng thước đo nhiều lần chiều dài cạnh lập lập phương; xử lí số liệu thí nghiệm xác định thể tích dựa vào công thức V = a3 Đáp án: A
Câu 4 :
Độ dịch chuyển và quãng đường đi được của vật có độ lớn bằng nhau khi vật
Đáp án : B Phương pháp giải :
Vận dụng kiến thức về Độ dịch chuyển và quãng đường đi được Lời giải chi tiết :
Độ dịch chuyển và quãng đường đi được của vật có độ lớn bằng nhau khi vật chuyển động thẳng và không đổi chiều Đáp án: B
Câu 5 :
Một con kiến bò quanh miệng của một cái bát được đúng 1 vòng. Đường kính của miệng chén là 6 cm. Độ dịch chuyển của con kiến là
Đáp án : C Phương pháp giải :
Vận dụng kiến thức về độ dịch chuyển Lời giải chi tiết :
Vì kiến đi được 1 vòng nên điểm đầu và điểm cuối trùng nhau à d = 0 m. Đáp án: C
Câu 6 :
Một con kiến bò quanh miệng của một cái bát được đúng 1 vòng. Đường kính của miệng chén là 6 cm. Độ dịch chuyển của con kiến là
Đáp án : C Phương pháp giải :
Vận dụng kiến thức về độ dịch chuyển Lời giải chi tiết :
Vì kiến đi được 1 vòng nên điểm đầu và điểm cuối trùng nhau à d = 0 m. Đáp án: C
Câu 7 :
Một người sử dụng google map để tra đường đi từ Trường THPT Quế võ số 2 đến ngã tư Phố mới thuộc thành phố Bắc Ninh được kết quả như hình vẽ bên dưới. Để đúng như bản đồ gợi ý, quãng đường dài 5,7 km, thời gian đi là 8 phút thì người đó phải di với tốc độ trung bình bằng
Đáp án : D Phương pháp giải :
Vận dụng kiến thức về tốc độ trung bình Lời giải chi tiết :
Tốc độ trung bình là: \(\overline v = \frac{{5,7}}{{\frac{8}{{60}}}} = 42,75km/h\) Đáp án: D
Câu 8 :
Trong hệ tọa độ vOt, với Ov là trục vận tốc và Ot là trục thời gian. Đồ thị vận tốc theo thời gian của chuyển động thẳng đều là
Đáp án : C Phương pháp giải :
Vận dụng kiến thức về Đồ thị vận tốc theo thời gian Lời giải chi tiết :
Đồ thị vận tốc theo thời gian của chuyển động thẳng đều là một đường thẳng song song trục hoành \(Ot.\) Đáp án: C
Câu 9 :
Người ngồi trên tàu A đang đi vào ga thấy cây bên đường và tàu B đang chuyển động giống nhau với cùng vận tốc. Vậy xe B và xe A có tính chất chuyển động thế nào?
Đáp án : A Phương pháp giải :
Vận dụng kiến thức về tính chất chuyển động Lời giải chi tiết :
Xe A chuyển động, xe B đứng yên Đáp án: A
Câu 10 :
Đơn vị của gia tốc là
Đáp án : A Phương pháp giải :
Vận dụng kiến thức về gia tốc Lời giải chi tiết :
Đơn vị của gia tốc là \({\rm{m/}}{{\rm{s}}^{\rm{2}}}{\rm{.}}\) Đáp án: A
Câu 11 :
Câu nào sai? Trong chuyển động thẳng nhanh dần đều thì
Đáp án : D Phương pháp giải :
Vận dụng kiến thức về chuyển động thẳng nhanh dần đều Lời giải chi tiết :
Trong chuyển động thẳng nhanh dần đều thì vectơ gia tốc cùng chiều với vectơ vận tốc Đáp án: D
Câu 12 :
Quá trình xe máy tăng tốc khi bắt đầu di chuyển và quá trình xe máy giảm tốc khi muốn dừng lại trong thời gian ngắn lần lượt tương ứng với chuyển động
Đáp án : A Phương pháp giải :
Vận dụng kiến thức về chuyển động biến đổi Lời giải chi tiết :
Quá trình xe máy tăng tốc khi bắt đầu di chuyển và quá trình xe máy giảm tốc khi muốn dừng lại trong thời gian ngắn lần lượt tương ứng với chuyển động nhanh dần và chậm dần Đáp án: A
Câu 13 :
Rơi tự do là chuyển động
Đáp án : B Phương pháp giải :
Vận dụng kiến thức về Rơi tự do Lời giải chi tiết :
Rơi tự do là chuyển động thẳng chậm dần đều Đáp án: B
Câu 14 :
Một vật rơi tự do từ một độ cao \(h.\) Biết rằng trong giây cuối cùng vật rơi được quãng đường \(25\,m.\) Lấy \(g = 10\,m{\rm{/}}{s^2}.\) Thời gian rơi của vật là
Đáp án : D Phương pháp giải :
Vận dụng kiến thức về rơi tự do Lời giải chi tiết :
Gọi t là thời gian rơi của vật ta có \(h = \frac{1}{2}g{t^2}\) Ta có : \(25 = \frac{1}{2}g{t^2} - \frac{1}{2}g{\left( {t - 1} \right)^2}25 = 5{t^2} - 5{\left( {t - 1} \right)^2} \Leftrightarrow 10t = 30 \Rightarrow t = 3{\rm{ }}s\) Đáp án: D
Câu 15 :
Một tàu vũ trụ đang di chuyển qua bề mặt của một tiểu hành tinh có khối lượng rất nhỏ. Tàu thả rơi một mẫu vật từ độ cao 50 m so với bề mặt của tiểu hành tinh. Gia tốc trọng trường trên tiểu hành tinh là g = 0,3 m/s2. Mẫu vật chạm bề mặt hành tinh sau
Đáp án : D Phương pháp giải :
Vận dụng kiến thức về rơi tự do Lời giải chi tiết :
Gọi t là thời gian rơi của vật ta có \(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.50}}{{0,3}}} \approx 18,26(s)\) Đáp án: D
Câu 16 :
Một cầu thủ bóng đá thực hiện cú ném biên với vận tốc ban đầu là 10 m/s ở độ cao 2 m so với mặt đất. Lấy g = 9,8 m/s2, bỏ qua lực cản của không khí, khoảng cách mà quả bóng sẽ rơi xuống đất theo phương ngang tính từ vị trí ném là
Đáp án : B Phương pháp giải :
Vận dụng kiến thức về ném ngang Lời giải chi tiết :
Gọi t là thời gian rơi của vật ta có \(L = {v_0}\sqrt {\frac{{2h}}{g}} = 10\sqrt {\frac{{2.2}}{{9,8}}} \approx 6,39(m)\) Đáp án: B
Câu 17 :
Để xác định vi phạm về tốc độ của các phương tiện giao thông đang di chuyển trên các tuyến đường, cảnh sát giao thông sử dụng
Đáp án : B Phương pháp giải :
Vận dụng kiến thức về an toàn giao thông Lời giải chi tiết :
Để xác định vi phạm về tốc độ của các phương tiện giao thông đang di chuyển trên các tuyến đường, cảnh sát giao thông sử dụng đồng hồ đo tốc độ bắn laser Đáp án: B
Câu 18 :
Một vật được thả từ độ cao 1,6 m trên mặt trăng, nơi gia tốc trong trường là g ≈ 1,6 m/s2. Một nhà khoa học đo thời gian vật rơi và thu được kết quả là 1,1 s. Dựa trên kết quả tính toán gia tốc thực nghiệm và so sánh với gia tốc lí thuyết, kết luận nào sau đây là đúng?
Đáp án : B Phương pháp giải :
Vận dụng kiến thức về gia tốc Lời giải chi tiết :
Gia tốc tính bằng thực nghiệm: \(g = \frac{{2h}}{g} = \frac{{2.1,6}}{{1,{1^2}}} \approx 2,64(m/{s^2})\) Kết luận: Gia tốc thực nghiệm lớn hơn gia tốc lí thuyết do sai số của phép đo thời gian. Đáp án: B
PHẦN II. CÂU TRẮC NGHIỆM ĐÚNG SAI.
Câu 1 :
Trong thí nghiệm đo gia tốc rơi tự do tại nơi có gia tốc rơi tự do g = 9,8 m/s2, bạn thực hiện 5 lần thí nghiệm và ghi lại thời gian rơi của vật thể. Biết sai số lấy một vạch chia nhỏ nhất. Bảng kết quả được ghi lại như sau
a) Chuyển động rơi tự do là chuyển động thẳng nhanh dần đều với gia tốc g.
Đúng
Sai
b) Kết quả đo thời gian \(\bar t\)= 1,44 (s).
Đúng
Sai
c) Kết quả giá trị trung bình của gia tốc rơi tự do vào khoảng: 9,6 m/s2
Đúng
Sai
d) Giá trị thực nghiệm khác giá trị lí thuyết là chủ yếu do sai số dụng cụ khi thực hiện phép đo thời gian.
Đúng
Sai
Đáp án
a) Chuyển động rơi tự do là chuyển động thẳng nhanh dần đều với gia tốc g.
Đúng
Sai
b) Kết quả đo thời gian \(\bar t\)= 1,44 (s).
Đúng
Sai
c) Kết quả giá trị trung bình của gia tốc rơi tự do vào khoảng: 9,6 m/s2
Đúng
Sai
d) Giá trị thực nghiệm khác giá trị lí thuyết là chủ yếu do sai số dụng cụ khi thực hiện phép đo thời gian.
Đúng
Sai
Phương pháp giải :
Vận dụng kiến thức về sai số trong thí nghiệm Lời giải chi tiết :
a) Đúng. b) \(\overline t = \frac{{1,4 + 1,5 + 1,3 + 1,6 + 1,4}}{5} = 1,44\)(s) à Đúng. c) Gia tốc rơi tự do: \(\bar g = \frac{{2\overline h }}{{{t^2}}} = \frac{{2.10,0}}{{{{(1,4)}^2}}} \approx 10,20408(m/{s^2})\)à Sai. d) Giá trị thực nghiệm khác giá trị lí thuyết là chủ yếu do sai số ngẫu nhiên khi thực hiện phép đo thời gian à Sai.
Câu 2 :
Một vận động viên bơi về phía Bắc với vận tốc 1,7 m/s. Nước sông chảy với vận tốc 1 m/s về phía Đông. Thời gian bơi của vận động viên là 15 phút. a) Vận động viên bơi đến bờ bên kia sẽ bị lệch về phía Đông so với điểm xuất phát
Đúng
Sai
b) Vận tốc của vận động viên so với bờ vào khoảng 1,97 m/s
Đúng
Sai
c) Để bơi đến đúng điểm đích thì vận động viên phải xuất phát từ điểm cách điểm đích theo phía Đông khoảng 0,25 m
Đúng
Sai
d) Để tiết kiệm sức nhất, vận động viên nên bơi ngược chiều dòng nước
Đúng
Sai
Đáp án
a) Vận động viên bơi đến bờ bên kia sẽ bị lệch về phía Đông so với điểm xuất phát
Đúng
Sai
b) Vận tốc của vận động viên so với bờ vào khoảng 1,97 m/s
Đúng
Sai
c) Để bơi đến đúng điểm đích thì vận động viên phải xuất phát từ điểm cách điểm đích theo phía Đông khoảng 0,25 m
Đúng
Sai
d) Để tiết kiệm sức nhất, vận động viên nên bơi ngược chiều dòng nước
Đúng
Sai
Phương pháp giải :
Vận dụng kiến thức về chuyển động Lời giải chi tiết :
a) Đúng. b) c) Theo phía Nam => Sai. d) Cùng chiều dòng nước thì vận tốc sẽ tăng lên => Sai.
Câu 3 :
Từ độ cao \(h = 1,6(m)\), người ta ném một quả bóng theo phương ngang với vận tốc ban đầu \({{\rm{v}}_{\rm{0}}}{\rm{ = 20 m/s}}\) vào một chiếc rổ. Lấy \({\rm{g = 10 m/}}{{\rm{s}}^{\rm{2}}}{\rm{.}}\) a) Theo phương ngang, vật chuyển động thẳng đều với vận tốc 20 m/s.
Đúng
Sai
b) Quỹ đạo chuyển động của quả bóng được nhìn thấy có dạng là đường thẳng.
Đúng
Sai
c) Thời gian rơi của vật lớn hơn thời gian rơi của vật nếu thả rơi từ đúng điểm ném
Đúng
Sai
d) Để vật rơi trúng rổ thì rổ phải đặt cách điểm ném theo phương ngang một đoạn 8\(\sqrt 2 \)m.
Đúng
Sai
Đáp án
a) Theo phương ngang, vật chuyển động thẳng đều với vận tốc 20 m/s.
Đúng
Sai
b) Quỹ đạo chuyển động của quả bóng được nhìn thấy có dạng là đường thẳng.
Đúng
Sai
c) Thời gian rơi của vật lớn hơn thời gian rơi của vật nếu thả rơi từ đúng điểm ném
Đúng
Sai
d) Để vật rơi trúng rổ thì rổ phải đặt cách điểm ném theo phương ngang một đoạn 8\(\sqrt 2 \)m.
Đúng
Sai
Phương pháp giải :
Vận dụng kiến thức về chuyển động ném ngang Lời giải chi tiết :
a) Đúng. b) Quỹ đạo có dạng là một phần của parabol => Sai. c) Thời gian rơi của vật bằng thời gian rơi của vật nếu thả rơi từ đúng điểm ném => Sai. d) \(L = {v_0}\sqrt {\frac{{2h}}{g}} = 20\sqrt {\frac{{2.1,6}}{{10}}} = 8\sqrt 2 (m)\)=> Đúng.
Câu 4 :
Một ô tô đang chạy với tốc độ \(54\;{\rm{km/h}}\) trên đoạn đường thẳng thì người lái xe hãm phanh cho ô tô chạy thẳng chậm dần đều để vào chỗ đỗ xe. Sau khi chạy thêm \(250\;{\rm{m}}\) thì tốc độ của ô tô chỉ còn \(5\;\;{\rm{m/s}}{\rm{.}}\) Biết chỗ xe cách người 300 m. a) Độ dịch chuyển của điện thoại khi chạm đất là d = 250 m.
Đúng
Sai
b) Ô tô từ khi hãm phan chuyển động với gia tốc có độ lớn 0,4 m/s2.
Đúng
Sai
c) Thời gian ô tô chạy thêm 250 m kể từ khi hãm phanh là 20 s.
Đúng
Sai
d) Ô tô dừng lại trước khi đến chỗ cần đỗ xe
Đúng
Sai
Đáp án
a) Độ dịch chuyển của điện thoại khi chạm đất là d = 250 m.
Đúng
Sai
b) Ô tô từ khi hãm phan chuyển động với gia tốc có độ lớn 0,4 m/s2.
Đúng
Sai
c) Thời gian ô tô chạy thêm 250 m kể từ khi hãm phanh là 20 s.
Đúng
Sai
d) Ô tô dừng lại trước khi đến chỗ cần đỗ xe
Đúng
Sai
Phương pháp giải :
Vận dụng kiến thức về độ dịch chuyển Lời giải chi tiết :
a) Đúng. b) \(a = \frac{{v_2^2 - v_1^2}}{{2d}} = \frac{{{5^2} - {{15}^2}}}{{2.250}} = - \,0,4\,(m/{s^2})\)=> Đúng. c) \(v_2^{} = v_1^{} + 2{\rm{a}}t\, \Rightarrow t = \frac{{v_2^{} - v_1^{}}}{a} = \frac{{5 - 15}}{{ - 0,4}} = 25{\rm{ s}}{\rm{.}}\)=> Sai. d) \(d = \frac{{v_3^2 - v_1^2}}{{2a}} = \frac{{{0^2} - {{15}^2}}}{{2.( - 0,4)}} = 281,25\,(m)\)=> Đúng.
PHẦN III. CÂU TRẮC NGHIỆM TRẢ LỜI NGẮN.
Phương pháp giải :
Vận dụng kiến thức về khái quát về Vật lí Lời giải chi tiết :
3 giai đoạn: Tiền Vật lí, Vật lí cổ điển, Vật lí hiện đại Đáp án: 3
Câu 2 :
Trong một lần thử xe ô tô, người ta xác định được độ dịch chuyển của xe theo thời gian như bảng sau.
Biết xe chuyển động thẳng theo một chiều nhất định. Vận tốc trung bình của ô tô trong 3 giây đầu tiên, trong 3 giây cuối cùng lần lượt là\({v_1},{v_2}\). Tổng \(\left( {{v_1} + 2{v_2}} \right)\) bằng bao nhiêu m/s? (Kết quả lấy đến phần nguyên). Phương pháp giải :
Vận dụng kiến thức về vận tốc Lời giải chi tiết :
Ta có \(\left\{ \begin{array}{l}{v_1} = \frac{{20,7}}{3} = 6,{\rm{9 m/s}}\\{v_2} = \frac{{\Delta d}}{{\Delta t}} = \frac{{57,6 - 9,2}}{3} = \frac{{{\rm{242}}}}{{{\rm{15}}}}{\rm{ m/s}}\end{array} \right. \Rightarrow {v_1} + 2{v_2} = 39,17{\rm{ m/s}}{\rm{.}}\) Đáp án: 39 Phương pháp giải :
Vận dụng kiến thức về chuyển động Lời giải chi tiết :
Ta có: t = t1 + t2 = \(\frac{{20}}{{40}} + \frac{{10}}{{20}} = 0,5 + 0,5 = 1(h)\) Người đó đến công ty lúc 8 h 00 phút sáng nên bị phạt 15.0 = 0 đồng Đáp án: 0 Phương pháp giải :
Vận dụng kiến thức về công thức tính gia tốc Lời giải chi tiết :
\(v{\rm{ }} = {\rm{ }}{v_0} + {\rm{ }}at \Rightarrow a = \frac{{v - {v_0}}}{t} = \frac{{0 - \left( { - 20} \right)}}{4} = 5{\rm{ m/}}{{\rm{s}}^{\rm{2}}}\) Đáp án: 5 Phương pháp giải :
Vận dụng kiến thức về ném ngang Lời giải chi tiết :
Vận tốc của vật khi chạm đất \(v = \sqrt {v_x^2 + v_y^2} = \sqrt {v_0^2 + 2gh} = \sqrt {{{20}^2} + 2.10.20} \, \approx 28,3({\rm{m/s)}}{\rm{.}}\) Đáp án: 28,3 Phương pháp giải :
Vận dụng kiến thức về chuyển động chậm dần đều Lời giải chi tiết :
s = s1 + s2 = v.t + \(\frac{{{v^2} - v_0^2}}{{2a}} = \frac{{60}}{{3,6}}.1 + \frac{{{0^2} - {{(\frac{{60}}{{3,6}})}^2}}}{{2.( - 4)}} \approx 51,4(m)\) Đáp án: 51,1
|
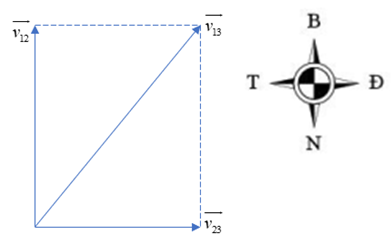=> \({v_{13}} = \sqrt {v_{12}^2 + v_{23}^2} = \sqrt {1,{7^2} + {1^2}} \approx 1,97(m/s)\)=> Đúng.
