Phương pháp giải:

Tính \(f'\left( x \right)\) sau đó giải bất phương trình \(f'\left( x \right) < 0\)

Lời giải chi tiết:

Có: \(f'\left( x \right) = 3{x^2} - 3.2x = 3{x^2} - 6x\)

\(f'\left( x \right) < 0 \Leftrightarrow 3{x^2} - 6x < 0 \Leftrightarrow 0 < x < 2\)

Chọn A.

Phương pháp giải:

Sử dụng khai triển hằng đẳng thức \({\left( {a + b} \right)^3}\), đưa các hạng tử về dạng \({x^n}\) và sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\).

Lời giải chi tiết:

\(\eqalign{  & f\left( x \right) = {\left( {\sqrt x  - {1 \over {\sqrt x }}} \right)^3} = {\left( {\sqrt x } \right)^3} - 3{\left( {\sqrt x } \right)^2}.{1 \over {\sqrt x }} + 3\sqrt x {\left( {{1 \over {\sqrt x }}} \right)^2} - {\left( {{1 \over {\sqrt x }}} \right)^3}  \cr   & f\left( x \right) = {x^{{3 \over 2}}} - 3\sqrt x  + {3 \over {\sqrt x }} - {1 \over {{x^{{3 \over 2}}}}}  \cr   & f\left( x \right) = {x^{{3 \over 2}}} - 3\sqrt x  + 3{x^{ - {1 \over 2}}} - {x^{ - {3 \over 2}}}  \cr   & f'\left( x \right) = {3 \over 2}{x^{{3 \over 2} - 1}} - {3 \over {2\sqrt x }} + 3.\left( { - {1 \over 2}} \right){x^{ - {1 \over 2} - 1}} + {3 \over 2}{x^{ - {3 \over 2} - 1}}  \cr   & f'\left( x \right) = {3 \over 2}\sqrt x  - {3 \over {2\sqrt x }} - {3 \over 2}{x^{ - {3 \over 2}}} + {3 \over 2}{x^{ - {5 \over 2}}}  \cr   & f'\left( x \right) = {3 \over 2}\left( {\sqrt x  - {1 \over {\sqrt x }} - {1 \over {x\sqrt x }} + {1 \over {{x^2}\sqrt x }}} \right) \cr} \)

Chọn D.

Phương pháp giải:

Sử dụng đạo hàm của hàm số hợp và các quy tắc tính đạo hàm tính đạo hàm của hàm số f(2x).

Thay x = 0 và suy ra \(f'\left( 0 \right)\)

Lời giải chi tiết:

\(\begin{array}{l}f'\left( {2x} \right).\left( {2x} \right)' = 4\left( {\cos x} \right)'.f\left( x \right) + 4\cos x.f'\left( x \right) - 2\\ \Rightarrow 2f'\left( {2x} \right) =  - 4\sin x.f\left( x \right) + 4\cos x.f'\left( x \right) - 2\\ \Rightarrow 2f'\left( 0 \right) = 4.f'\left( 0 \right) - 2\\ \Leftrightarrow f'\left( 0 \right) = 1\end{array}\)

Chọn B.

Phương pháp giải:

Xét tổng:

\(\begin{align}  f(x)\,\,\,\,\,=1+x+{{x}^{2}}+{{x}^{3}}+...+{{x}^{n}} \\  f'(x)\,\,\,=\,\,\,\,\,\,\,\,\,1\,+2x+3{{x}^{2}}+...+n{{x}^{n-1}}. \\ \end{align}\)

Áp dụng công thức tính tổng của cấp số nhân.

Lời giải chi tiết:

\(f(x)=1+x+{{x}^{2}}+{{x}^{3}}+...+{{x}^{n}}=\frac{{{x}^{n+1}}-1}{x-1},\,\,\,(x\ne 1)\)

\(\begin{align}  f'(x)=1+2x+3{{x}^{2}}+...+n{{x}^{n-1}}=\frac{(n+1){{x}^{n}}(x-1)-({{x}^{n+1}}-1)}{{{\left( x-1 \right)}^{2}}}\\=\frac{(n+1){{x}^{n+1}}-(n+1){{x}^{n}}-{{x}^{n+1}}+1}{{{\left( x-1 \right)}^{2}}}=\frac{n{{x}^{n+1}}-(n+1){{x}^{n}}+1}{{{\left( x-1 \right)}^{2}}} \\ \end{align}\)

Cho \(x=2,\,\,n=2018\), ta có: \(S=1+2.2+{{3.2}^{2}}+{{4.2}^{3}}+...+{{2018.2}^{2017}}=\frac{{{2018.2}^{2019}}-{{2019.2}^{2018}}+1}{{{\left( 2-1 \right)}^{2}}}\\={{2}^{2018}}\left( 2018.2-2019 \right)+1={{2017.2}^{2018}}+1\)

Chọn: A

Phương pháp giải:

Sử dụng công thức tính đạo của 1 tích : \(\left( {uv} \right)' = u'v + uv'\) và cách tính đạo hàm của hàm số hợp.

Lời giải chi tiết:

\(\eqalign{  & f'\left( x \right) = \left( {{x^2} - 3} \right)'.\sqrt {{x^2} - 2x + 4}  + \left( {{x^2} - 3} \right).\left( {\sqrt {{x^2} - 2x + 4} } \right)'  \cr   &  = 2x\sqrt {{x^2} - 2x + 4}  + \left( {{x^2} - 3} \right).{{\left( {{x^2} - 2x + 4} \right)'} \over {2\sqrt {{x^2} - 2x + 4} }}  \cr   &  = 2x\sqrt {{x^2} - 2x + 4}  + \left( {{x^2} - 3} \right).{{2x - 2} \over {2\sqrt {{x^2} - 2x + 4} }}  \cr   &  = 2x\sqrt {{x^2} - 2x + 4}  + {{\left( {x - 1} \right)\left( {{x^2} - 3} \right)} \over {\sqrt {{x^2} - 2x + 4} }} \cr} \).

Chọn A.

Phương pháp giải:

+) Sử dụng bảng đạo hàm cơ bản \(\left( {{x^n}} \right)' = n{x^{n - 1}}\) và quy tắc đạo hàm của một tích \(\left( {uv} \right)' = u'v + uv'\).

+) Thay \(x = 1\) vào \(f'\left( x \right)\).

Lời giải chi tiết:

Ta có:

\(f'\left( x \right) = 1.\sqrt x  + x.\dfrac{1}{{2\sqrt x }} + 2x \Rightarrow f'\left( 1 \right) = 1 + \dfrac{1}{2} + 2 = \dfrac{7}{2}\).

Chọn C.

Phương pháp giải:

Tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) có \(\Delta  < 0\) thì luôn cùng dấu với hệ số \(a\).

Lời giải chi tiết:

Ta có \(f'\left( x \right) =  - 3{x^2} + 6mx - 12\).

\(f'\left( x \right) < 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \Delta ' < 0 \Leftrightarrow {\left( {3m} \right)^2} - 36 < 0 \Leftrightarrow {m^2} < 4 \Leftrightarrow  - 2 < m < 2\).

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 2; - 1;0;1;2} \right\}\).

Chọn B.

Phương pháp giải:

Sử dụng công thức \(\left( {{x^n}} \right)' = n.{x^{n - 1}}\) và \(\left( {\sqrt u } \right)' = \dfrac{{u'}}{{2\sqrt u }}\) tính \(f'\left( x \right)\). Từ đó giải bất phương trình.

Lời giải chi tiết:

Ta có \(f'\left( x \right) = 1 + \dfrac{{2x}}{{2\sqrt {{x^2} + 1} }} = 1 + \dfrac{x}{{\sqrt {{x^2} + 1} }}\).

Theo bài ra ta có \(2x.f'\left( x \right) - f\left( x \right) \ge 0\)

\(\begin{array}{l} \Leftrightarrow 2x\left( {1 + \dfrac{x}{{\sqrt {{x^2} + 1} }}} \right) - x - \sqrt {{x^2} + 1}  \ge 0\\ \Leftrightarrow 2x + \dfrac{{2{x^2}}}{{\sqrt {{x^2} + 1} }} - x - \sqrt {{x^2} + 1}  \ge 0\\ \Leftrightarrow \dfrac{{2x\sqrt {{x^2} + 1}  + 2{x^2} - x\sqrt {{x^2} + 1}  - {x^2} - 1}}{{\sqrt {{x^2} + 1} }} \ge 0\\ \Leftrightarrow g\left( x \right) = {x^2} - 1 + x\sqrt {{x^2} + 1}  \ge 0\end{array}\)

Thử các đáp án:

Với \(x = \dfrac{1}{{\sqrt 3 }} \Rightarrow g\left( x \right) = 0 \Rightarrow x = \dfrac{1}{{\sqrt 3 }}\) thuộc tập nghiệm của BPT \( \Rightarrow \) Loại đáp án A, B và C.

Chọn D.

Phương pháp giải:

Sử dụng công thức tính đạo hàm \(\left( {\sqrt u } \right)' = \dfrac{{u'}}{{2\sqrt u }}\).

Lời giải chi tiết:

Ta có: \(f'\left( x \right) = \dfrac{{\left[ {{{\left( {2 - 5x} \right)}^3}} \right]'}}{{2\sqrt {{{\left( {2 - 5x} \right)}^3}} }} = \dfrac{{3{{\left( {2 - 5x} \right)}^2}\left( { - 5} \right)}}{{2\sqrt {{{\left( {2 - 5x} \right)}^3}} }} = \dfrac{{ - 15{{\left( {2 - 5x} \right)}^2}}}{{2\sqrt {{{\left( {2 - 5x} \right)}^3}} }}\)

\( \Rightarrow a =  - 15,\,\,b = 2 \Rightarrow P = ab =  - 30\).

Chọn C.

Phương pháp giải:

Sử dụng công thức tính đạo hàm của tích \(\left( {uv} \right)' = u'v + uv'\).

Lời giải chi tiết:

Ta có \(g'\left( x \right) = f\left( x \right) + xf'\left( x \right) + 1\).

\( \Rightarrow g'\left( 3 \right) = f\left( 3 \right) + 3f'\left( 3 \right) + 1 \Leftrightarrow 2 = f\left( 3 \right) + 3.\left( { - 1} \right) + 1 \Leftrightarrow f\left( 3 \right) = 4\)

\( \Rightarrow g\left( 3 \right) = 3f\left( 3 \right) + 3 = 3.4 + 3 = 15\) .

Chọn D.

Phương pháp giải:

Sử dụng quy tắc tính đạo hàm của thương: \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\).

Lời giải chi tiết:

\(\begin{array}{l}y' = \dfrac{{\left( {2x - 3} \right)\left( {{x^2} + x - 2} \right) - \left( {{x^2} - 3x + 4} \right)\left( {2x + 1} \right)}}{{{{\left( {{x^2} + x - 2} \right)}^2}}}\\y' = \dfrac{{2{x^3} + 2{x^2} - 4x - 3{x^2} - 3x + 6 - 2{x^3} + 6{x^2} - 8x - {x^2} + 3x - 4}}{{{{\left( {{x^2} + x - 2} \right)}^2}}}\\y' = \dfrac{{4{x^2} - 12x + 2}}{{{{\left( {{x^2} + x - 2} \right)}^2}}}\end{array}\)

Chọn D.

Phương pháp giải:

Hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có \(y' \ge 0\,\,\forall x \in \left( {a;b} \right) \Leftrightarrow \left\{ \begin{array}{l}y' \ge 0\,\\ - \dfrac{d}{c} \notin \left( {a;b} \right)\end{array} \right.\).

Lời giải chi tiết:

Ta có: \(y' = \dfrac{{ - {m^2} - {m^2} - 10m + 12}}{{{{\left( {x - m} \right)}^2}}} = \dfrac{{ - 2{m^2} - 10m + 12}}{{{{\left( {x - m} \right)}^2}}}\).

\(y' \ge 0\,\,\forall x \in \left( { - \infty ; - 4} \right) \Leftrightarrow \left\{ \begin{array}{l} - 2{m^2} - 10m + 12 \ge 0\\m \notin \left( { - \infty ; - 4} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 6 \le m \le 1\\m \ge  - 4\end{array} \right. \Leftrightarrow  - 4 \le m \le 1\).

Mà \(m \in \mathbb{Z} \Rightarrow m \in \left\{ { - 4; - 3; - 2; - 1;0;1} \right\}\). Vậy có 6 giá trị của \(m\) thỏa mãn. Chọn C.

Phương pháp giải:

Sử dụng công thức tính đạo hàm hàm hợp \(\left[ {f\left( u \right)} \right]' = f'\left( u \right).u'\).

Lời giải chi tiết:

\(g\left( x \right) = f\left( {1 - {x^2}} \right) \Leftrightarrow g'\left( x \right) = f'\left( {1 - {x^2}} \right).\left( { - 2x} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\f'\left( {1 - {x^2}} \right) = 0\,\,\left( * \right)\end{array} \right.\)

Ta có: \(f'\left( x \right) = {x^2} - 4x - 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 6\\x =  - 2\end{array} \right.\)

Do đó \(\left( * \right) \Leftrightarrow \left[ \begin{array}{l}1 - {x^2} = 6\\1 - {x^2} =  - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} =  - 5\,\,\left( {vo\,\,nghiem} \right)\\{x^2} = 3\end{array} \right. \Leftrightarrow x =  \pm \sqrt 3 \).

Vậy phương trình \(g'\left( x \right) = 0\) có 3 nghiệm \(x = 0,\,\,x =  \pm \sqrt 3 \).

Chọn D.

Phương pháp giải:

+) Sử dụng các công thức đạo hàm cơ bản tính \(f'\left( x \right)\).

+) Tam thức bậc hai \(a{x^2} + bx + c\,\,\left( {a \ne 0} \right)\) có \(\Delta  < 0\) thì luôn cùng dấu với hệ số \(a\).

Lời giải chi tiết:

Ta có \(f'\left( x \right) = m{x^2} - mx + 3 - m\).

\(\begin{array}{l}f'\left( x \right) > 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m = 0\\f'\left( x \right) = 3 > 0\,\,\forall x \in \mathbb{R}\end{array} \right.\\\left\{ \begin{array}{l}m \ne 0\\1 > 0\,\,\left( {luon\,\,dung} \right)\\\Delta  = {m^2} - 4m\left( {3 - m} \right) < 0\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\\5{m^2} - 12m < 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\0 < m < \dfrac{{12}}{5}\end{array} \right. \Leftrightarrow 0 \le m < \dfrac{{12}}{5}\end{array}\).

Chọn C.

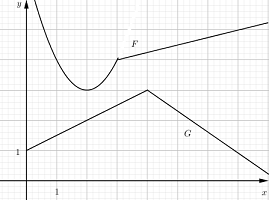
Phương pháp giải:

Tốc độ tăng nhiệt tại thời điểm \(t = {t_0}\) là \(f'\left( {{t_0}} \right)\).

Lời giải chi tiết:

Ta có \(f'\left( t \right) = 3{\left( {t - 1} \right)^2}\).

Tốc độ tăng nhiệt tại thời điểm \({t_1} = 0,5s\) là \(f'\left( {0,5} \right) = 0,75\).

Tốc độ tăng nhiệt tại thời điểm \({t_2} = 1,25s\) là \(f'\left( {1,25} \right) = 0,1875\).

Vậy nhiệt độ tại thời điểm \({t_1}\) tăng nhanh hơn tại thời điểm \({t_2}\).

Chọn A.

Phương pháp giải:

Sử dụng công thức tính đạo hàm của hàm số: \(\left[ {f\left( x \right).g\left( x \right)} \right]' = f'\left( x \right)g\left( x \right) + f\left( x \right).g'\left( x \right).\)

Lời giải chi tiết:

Xét khoảng \(\left( {0;\,3} \right)\) ta có: \(\left\{ \begin{array}{l}F\left( x \right) = {x^2} - 4x + 7\\G\left( x \right) = \dfrac{1}{2}x + 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}F'\left( x \right) = 2x - 4\\G'\left( x \right) = \dfrac{1}{2}\end{array} \right.\)

Ta có: \(P\left( x \right) = F\left( x \right).G\left( x \right)\)

\(\begin{array}{l} \Rightarrow P'\left( x \right) = F'\left( x \right).G\left( x \right) + F\left( x \right).G'\left( x \right)\\ \Rightarrow P'\left( 2 \right) = F'\left( 2 \right).G\left( 2 \right) + F\left( 2 \right).G'\left( 2 \right)\\ = \left( {2.2 - 4} \right).2 + 3.\dfrac{1}{2} = \dfrac{3}{2}.\end{array}\)

Chọn C.

Phương pháp giải:

+) Sử dụng công thức tính đạo hàm \(\left( {{x^n}} \right)' = n{x^{n - 1}}\).

+) Giải bất phương trình \(y' \ge 0\,\,\forall x \in \mathbb{R}\).

Lời giải chi tiết:

Ta có \(y' = \left( {2m - 1} \right){x^2} - 2mx + 1\).

Ta có: \(y' \ge 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left( {2m - 1} \right){x^2} - 2mx + 1 \ge 0\,\,\forall x \in \mathbb{R}\,\,\left( * \right)\)

TH1: \(2m - 1 = 0 \Leftrightarrow m = \dfrac{1}{2}\).

Khi đó ta có \( - x + 1 \ge 1 \Leftrightarrow x \le 0\,\,\left( {ktm} \right)\).

TH2: \(2m - 1 \ne 0 \Leftrightarrow m \ne \dfrac{1}{2}\).

\(\left( * \right) \Leftrightarrow \left\{ \begin{array}{l}a = 2m - 1 > 0\\\Delta ' = {m^2} - \left( {2m - 1} \right) \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{1}{2}\\{\left( {m - 1} \right)^2} \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > \dfrac{1}{2}\\m = 1\end{array} \right. \Leftrightarrow m = 1\).

Vậy \(m=1\).

Phương pháp giải:

\(v\left( t \right) = s'\left( t \right),\,\,a\left( t \right) = v'\left( t \right)\).

Lời giải chi tiết:

Ta có \(a\left( t \right) = v'\left( t \right) = \left( {s'\left( t \right)} \right)' = s''\left( t \right)\)

\(v\left( t \right) = S'\left( t \right) = 3{t^2} + 6t - 9 \Rightarrow a\left( t \right) = S''\left( t \right) = 6t + 6\).

Giả sử \({t_0}\) là thởi điểm vận tốc của vật triệt tiêu \( \Rightarrow v\left( {{t_0}} \right) = 0\)

\( \Leftrightarrow 3t_0^2 + 6{t_0} - 9 = 0 \Leftrightarrow {t_0} = 1\).

Vậy giá tốc của vật tại thời điểm \({t_0} = 1\) là \(a\left( 1 \right) = 6.1 + 6 = 12\,\,\left( {m/{s^2}} \right)\).

Chọn D

Phương pháp giải:

Sử dụng quy tắc \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\).

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\). Ta có:

\(\begin{array}{l}y' = \dfrac{{\left( {2x + 3m - 2} \right)\left( {x + 2} \right) - \left( {{x^2} + \left( {3m - 2} \right)x + 1 - 2m} \right)}}{{{{\left( {x + 2} \right)}^2}}}\\y' = \dfrac{{2{x^2} + \left( {3m - 2} \right)x + 4x + 2\left( {3m - 2} \right) - {x^2} - \left( {3m - 2} \right)x - 1 + 2m}}{{{{\left( {x + 2} \right)}^2}}}\\y' = \dfrac{{{x^2} + 4x + 8m - 5}}{{{{\left( {x + 2} \right)}^2}}}\end{array}\)

\(y' \ge 0\,\,\forall x \in D \Leftrightarrow {x^2} + 4x + 8m - 5 \ge 0\,\,\forall x \ne  - 2\).

Ta có \(\Delta ' = 4 - 8m + 5 = 9 - 8m\).

TH1: \(\Delta ' < 0 \Rightarrow 9 - 8m < 0 \Leftrightarrow m > \dfrac{9}{8}\).

Khi đó \({x^2} + 4x + 8m - 5 \ge 0\,\,\forall x \ne \mathbb{R}\,\,\left( {tm} \right).\)

TH2: \(\Delta ' = 0 \Rightarrow 9 - 8m = 0 \Leftrightarrow m = \dfrac{9}{8}\).

Khi đó \({x^2} + 4x + 8m - 5 \ge 0\,\,\forall x \ne \dfrac{{ - 4}}{2} =  - 2\,\,\left( {tm} \right).\)

Vậy \(m \ge \dfrac{9}{8}\).

Chọn A.

Phương pháp giải:

Sử dụng công thức \(\left( {{u^n}} \right)' = n{u^{n - 1}}u'\).

Lời giải chi tiết:

\(y' = 3{\left( {2{x^2} + 1} \right)^2}\left( {2{x^2} + 1} \right)' = 12x{\left( {2{x^2} + 1} \right)^2}\).

\(y' \ge 0 \Leftrightarrow 2x{\left( {2{x^2} + 1} \right)^2} \ge 0\). Do \({\left( {2{x^2} + 1} \right)^2} \ge 0\,\,\forall x \Rightarrow y' \ge 0 \Leftrightarrow 2x \ge 0 \Leftrightarrow x \ge 0\).

Vậy \(x \in \left[ {0; + \infty } \right)\).

Chọn B

Phương pháp giải:

Tính \(f'\left( x \right)\) theo công thức \({\left( {\dfrac{1}{u}} \right)^\prime } =  - \dfrac{{u'}}{{{u^2}}}\)

Rồi giải bất phương trình \(f'\left( x \right) > 0\)

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\)

Ta có \(f'\left( x \right) = {\left( {\dfrac{1}{{{x^2} + 1}}} \right)^\prime } =  - \dfrac{{2x}}{{{{\left( {{x^2} + 1} \right)}^2}}}\)

Xét \(f'\left( x \right) > 0 \Leftrightarrow \dfrac{{ - 2x}}{{{{\left( {{x^2} + 1} \right)}^2}}} > 0 \Leftrightarrow  - 2x > 0 \Leftrightarrow x < 0\)

Vậy \(S = \left( { - \infty ;0} \right)\)

Chọn C.

Phương pháp giải:

Tính \(f'\left( x \right)\) rồi giải phương trình \(f'\left( x \right) = 0.\)

Sử dụng công thức đạo hàm \({\left( {\sqrt u } \right)^\prime } = \dfrac{{u'}}{{2\sqrt u }}\)

Lời giải chi tiết:

ĐK : \( - \sqrt 3  \le x \le \sqrt 3 \)

Ta có \(f'\left( x \right) = 2 + \dfrac{{ - 2x}}{{2\sqrt {3 - {x^2}} }} = 2 - \dfrac{x}{{\sqrt {3 - {x^2}} }}\)

Xét  

\( \Rightarrow 2\sqrt {3 - {x^2}}  = x \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\4\left( {3 - {x^2}} \right) = {x^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\5{x^2} = 12\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\\left[ \begin{array}{l}x = \sqrt {\dfrac{{12}}{5}} \\x =  - \sqrt {\dfrac{{12}}{5}} \end{array} \right.\end{array} \right. \Rightarrow x = \dfrac{{2\sqrt {15} }}{5}\,\left( {TM} \right)\)

Vậy \(x = \dfrac{{2\sqrt {15} }}{5}.\)

Phương pháp giải:

Sử dụng quy tắc tính đạo hàm \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\).

Lời giải chi tiết:

Ta có \(y' = \frac{{2x\left( {x + 1} \right) - \left( {{x^2} + 3} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{2{x^2} + 2x - {x^2} - 3}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2x - 3}}{{{{\left( {x + 1} \right)}^2}}}\)

\(y' > 0 \Leftrightarrow \frac{{{x^2} + 2x - 3}}{{{{\left( {x + 1} \right)}^2}}} > 0 \Leftrightarrow {x^2} + 2x - 3 > 0 \Leftrightarrow x \in \left( { - \infty ; - 3} \right) \cup \left( {1; + \infty } \right)\).

Chọn A.

Phương pháp giải:

Sử dụng quy tắc tính đạo hàm \(\left( {\dfrac{u}{v}} \right)' = \dfrac{{u'v - uv'}}{{{v^2}}}\).

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}y' = \dfrac{{\dfrac{{2x + 2}}{{2\sqrt {{x^2} + 2x + 3} }}.x - \sqrt {{x^2} + 2x + 3} }}{{{x^2}}}\\y' = \dfrac{{{x^2} + x - {x^2} - 2x - 3}}{{{x^2}\sqrt {{x^2} + 2x + 3} }} = \dfrac{{ - x - 3}}{{{x^2}\sqrt {{x^2} + 2x + 3} }}\\ \Rightarrow \left\{ \begin{array}{l}a =  - 1\\b =  - 3\end{array} \right. \Rightarrow \max \left\{ {a;b} \right\} = \max \left\{ { - 1; - 3} \right\} =  - 1\end{array}\)

Chọn B.

Phương pháp giải:

Sử dụng công thức tính đạo hàm hàm hợp: \(\left[ {f\left( u \right)} \right]' = u'.f'\left( u \right)\).

Lời giải chi tiết:

\(f\left( {3 - x} \right) = {x^2} + x \Rightarrow  - f'\left( {3 - x} \right) = 2x + 1\).

Thay \(x = 1\) ta có \( - f'\left( 2 \right) = 2.1 + 1 = 3 \Rightarrow f'\left( 2 \right) =  - 3\).

Chọn B.

Phương pháp giải:

+) Tính \(f'\left( x \right)\).

+) Giải BPT dạng \(\sqrt {f\left( x \right)}  > g\left( x \right) \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}f\left( x \right) \ge 0\\g\left( x \right) < 0\end{array} \right.\\\left\{ \begin{array}{l}g\left( x \right) \ge 0\\f\left( x \right) > {g^2}\left( x \right)\end{array} \right.\end{array} \right.\) .

Lời giải chi tiết:

\(\begin{array}{l}DKXD:\,\, - 1 \le x \le 1\\f'\left( x \right) = 2 + \dfrac{{ - 2x}}{{2\sqrt {1 - {x^2}} }} = 2 - \dfrac{x}{{\sqrt {1 - {x^2}} }}\\f'\left( x \right) > 0 \Leftrightarrow 2 - \dfrac{x}{{\sqrt {1 - {x^2}} }} > 0 \Leftrightarrow \dfrac{{2\sqrt {1 - {x^2}}  - x}}{{\sqrt {1 - {x^2}} }} > 0\,\,\left( {x \in \left( { - 1;1} \right)} \right)\\ \Leftrightarrow 2\sqrt {1 - {x^2}}  - x > 0 \Leftrightarrow 2\sqrt {1 - {x^2}}  > x\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}1 - {x^2} > 0\\x < 0\end{array} \right.\\\left\{ \begin{array}{l}x \ge 0\\4\left( {1 - {x^2}} \right) > {x^2}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l} - 1 < x < 1\\x < 0\end{array} \right.\\\left\{ \begin{array}{l}x \ge 0\\5{x^2} < 4\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 1 < x < 0\\\left\{ \begin{array}{l}x \ge 0\\\dfrac{{ - 2}}{{\sqrt 5 }} < x < \dfrac{2}{{\sqrt 5 }}\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} - 1 < x < 0\\0 \le x < \dfrac{2}{{\sqrt 5 }}\end{array} \right. \Leftrightarrow  - 1 < x < \dfrac{2}{{\sqrt 5 }}\,\,\left( {tm\,\,DKXD} \right)\end{array}\)

Vậy nghiệm của BPT là:  \(x \in \left( { - 1;\dfrac{2}{{\sqrt 5 }}} \right).\)

Chọn C.

Phương pháp giải:

Lời giải chi tiết:

Chọn D.

Phương pháp giải:

Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) là \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\) (nếu tồn tại).

Lời giải chi tiết:

\(f'\left( { - 1} \right) = \mathop {\lim }\limits_{x \to \left( { - 1} \right)} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}}\)

Ta có:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{\frac{{{x^2} + x + 1}}{x} + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{{x^2} + 2x + 1}}{{x\left( {x + 1} \right)}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{x + 1}}{x} = 0\\\mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{\frac{{{x^2} - x - 1}}{x} + 1}}{{x + 1}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{{x^2} - 1}}{{x\left( {x + 1} \right)}} = \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{x - 1}}{x} = 2\\ \Rightarrow \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ + }} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}} \ne \mathop {\lim }\limits_{x \to {{\left( { - 1} \right)}^ - }} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}}\end{array}\)

Do đó không tồn tại  \(\mathop {\lim }\limits_{x \to \left( { - 1} \right)} \frac{{f\left( x \right) - f\left( { - 1} \right)}}{{x + 1}}\), vậy không tồn tại đạo hàm của hàm số tại \({x_0} =  - 1\).

Chọn D.

Phương pháp giải:

Tính \(f'\left( x \right)\) sau đó giải bất phương trình \(f'\left( x \right) < 0\)

Lời giải chi tiết:

Có: \(f'\left( x \right) = 3{x^2} - 3.2x = 3{x^2} - 6x\)

\(f'\left( x \right) < 0 \Leftrightarrow 3{x^2} - 6x < 0 \Leftrightarrow 0 < x < 2\)

Chọn A.

Phương pháp giải:

Sử dụng khai triển hằng đẳng thức \({\left( {a + b} \right)^3}\), đưa các hạng tử về dạng \({x^n}\) và sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\) .

Lời giải chi tiết:

\(\begin{array}{l}f\left( x \right) = {\left( {\sqrt x  - \frac{1}{{\sqrt x }}} \right)^3} = {\left( {\sqrt x } \right)^3} - 3{\left( {\sqrt x } \right)^2}.\frac{1}{{\sqrt x }} + 3\sqrt x {\left( {\frac{1}{{\sqrt x }}} \right)^2} - {\left( {\frac{1}{{\sqrt x }}} \right)^3}\\f\left( x \right) = {x^{\frac{3}{2}}} - 3\sqrt x  + \frac{3}{{\sqrt x }} - \frac{1}{{{x^{\frac{3}{2}}}}}\\f\left( x \right) = {x^{\frac{3}{2}}} - 3\sqrt x  + 3{x^{ - \frac{1}{2}}} - {x^{ - \frac{3}{2}}}\\f'\left( x \right) = \frac{3}{2}{x^{\frac{3}{2} - 1}} - \frac{3}{{2\sqrt x }} + 3.\left( { - \frac{1}{2}} \right){x^{ - \frac{1}{2} - 1}} + \frac{3}{2}{x^{ - \frac{3}{2} - 1}}\\f'\left( x \right) = \frac{3}{2}\sqrt x  - \frac{3}{{2\sqrt x }} - \frac{3}{2}{x^{ - \frac{3}{2}}} + \frac{3}{2}{x^{ - \frac{5}{2}}}\\f'\left( x \right) = \frac{3}{2}\left( {\sqrt x  - \frac{1}{{\sqrt x }} - \frac{1}{{x\sqrt x }} + \frac{1}{{{x^2}\sqrt x }}} \right)\end{array}\)

Chọn D.

Phương pháp giải:

Đạo hàm của hàm số \(y = f\left( x \right)\) tại điểm \(x = {x_0}\) là \(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}}\)

Lời giải chi tiết:

\(\begin{array}{l}f'\left( 0 \right) = \mathop {\lim }\limits_{x \to 0} \frac{{f\left( x \right) - f\left( 0 \right)}}{{x - 0}} = \mathop {\lim }\limits_{x \to 0} \frac{{x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 1000} \right) - 0}}{x}\\ = \mathop {\lim }\limits_{x \to 0} \left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 1000} \right) = \mathop {\lim }\limits_{x \to 0} \left( { - 1} \right)\left( { - 2} \right)\left( { - 3} \right)...\left( { - 1000} \right) = {\left( { - 1} \right)^{1000}}.1000! = 1000!\end{array}\)

Chọn B.

Phương pháp giải:

- Tính đạo hàm của hàm số, sử dụng công thức đạo hàm cơ bản: \(\left( {{x^n}} \right)' = n{x^{n - 1}}\).

- Giải bất phương trình \(y' \le 0\), sử dụng quy tắc phải cùng, trái khác.

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\).

Ta có: \(y = \dfrac{1}{3}{x^3} - 2{x^2} + 3x + \dfrac{1}{3}\)\( \Rightarrow y' = {x^2} - 4x + 3\) 

Khi đó \(y' \le 0 \Leftrightarrow {x^2} - 4x + 3 \le 0 \Leftrightarrow 1 \le x \le 3\).

Vậy tập nghiệm của bất phương trình \(y' \le 0\) là \(\left[ {1;3} \right]\).

Chọn D.

Phương pháp giải:

- Tìm đạo hàm của hàm số. Sử dụng công thức \(\left( {{x^n}} \right)' = n{x^{n - 1}}\).

- Tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c \ge 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  \le 0\end{array} \right.\).

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\).

Ta có \(f'\left( x \right) = {x^2} - 2x + m\)

\(\begin{array}{l}f'\left( x \right) \ge 0\,\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow {x^2} - 2x + m \ge 0\,\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\\Delta ' = 1 - m \le 0\end{array} \right.\\ \Leftrightarrow m \ge 1.\end{array}\)

Chọn A.

Phương pháp giải:

Tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c \ge 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  \le 0\end{array} \right.\).

Lời giải chi tiết:

TXĐ: \(D = \mathbb{R}\).

Ta có:

\(\begin{array}{l}y = \dfrac{1}{3}{x^3} + \left( {2m + 1} \right){x^2} - mx - 4\\ \Rightarrow y' = {x^2} + 2\left( {2m + 1} \right)x - m\\ \Rightarrow y' \ge 0\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow {x^2} + 2\left( {2m + 1} \right)x - m \ge 0\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ \begin{array}{l}1 > 0\\\Delta ' = {\left( {2m + 1} \right)^2} + m \le 0\end{array} \right.\\ \Leftrightarrow 4{m^2} + 4m + 1 + m \le 0\\ \Leftrightarrow 4{m^2} + 5m + 1 \le 0\\ \Leftrightarrow  - 1 \le m \le  - \dfrac{1}{4}\end{array}\)

Vậy \(m \in \left[ { - 1; - \dfrac{1}{4}} \right]\).

Chọn C.

Phương pháp giải:

- Tìm ĐKXĐ.

- Sử dụng công thức \(\left( {\sqrt u } \right)' = \dfrac{{u'}}{{2\sqrt u }}\) để tính đạo hàm của hàm số.

- Giải bất phương trình, tìm nghiệm nguyên.

Lời giải chi tiết:

ĐKXĐ: \({x^2} + 2x \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 0\\x \le  - 2\end{array} \right.\).

Ta có: \(f'\left( x \right) = \dfrac{{2x + 2}}{{2\sqrt {{x^2} + 2x} }} = \dfrac{{x + 1}}{{\sqrt {{x^2} + 2x} }}\).

Khi đó \(f'\left( x \right) \ge f\left( x \right)\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{x + 1}}{{\sqrt {{x^2} + 2x} }} \ge \sqrt {{x^2} + 2x} \\ \Leftrightarrow x + 1 \ge {x^2} + 2x\\ \Leftrightarrow {x^2} + x - 1 \le 0\\ \Leftrightarrow \dfrac{{ - 1 - \sqrt 5 }}{2} \le x \le \dfrac{{ - 1 + \sqrt 5 }}{2}\end{array}\)

Kết hợp ĐKXĐ ta có: \(x \in \left( {\dfrac{{ - 1 - \sqrt 5 }}{2}; - 2} \right] \cup \left[ {0;\dfrac{{ - 1 + \sqrt 5 }}{2}} \right)\).

Suy ra phương trình trên có 2 nghiệm nguyên là \(x = 0,\,\,x =  - 2\).

Vậy số nghiệm nguyên của bất phương trình trên là 2.

Chọn D.

Phương pháp giải:

Tính đạo hàm của hàm hợp: \(\left( {{u^n}} \right)' = n.{u^{n - 1}}.u'\).

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}y = {\left( {{x^3} - 2{x^2}} \right)^{2019}}\\ \Rightarrow y' = 2019.{\left( {{x^3} - 2{x^2}} \right)^{2018}}.\left( {{x^3} - 2{x^2}} \right)'\\\,\,\,\,\,\,\,y' = 2019.{\left( {{x^3} - 2{x^2}} \right)^{2018}}.\left( {3{x^2} - 4x} \right)\end{array}\)

Lại có \(f\left( 2 \right) = m\).

Do đó để hàm số liên tục tại \(x = 2\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = f\left( 2 \right)\)\( \Leftrightarrow m = 3\).

Chọn C.

Phương pháp giải:

Tính \(f'\left( x \right)\).

Để \(a{x^2} + bx + c > 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  < 0\end{array} \right.\).

Lời giải chi tiết:

Ta có: \(f'\left( x \right) = m{x^2} - mx + 3 - m\).

\(f'\left( x \right) > 0\,\,\forall x \in \mathbb{R}\)

\(\begin{array}{l} \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}m = 0\\3 > 0\,\,\left( {luon\,\,dung} \right)\end{array} \right.\\\left\{ \begin{array}{l}m > 0\\\Delta  = {m^2} - m\left( {3 - m} \right) < 0\end{array} \right.\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > 0\\2{m^2} - 3m > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m > 0\\\left[ \begin{array}{l}m > \dfrac{3}{2}\\m < 0\end{array} \right.\end{array} \right. \Leftrightarrow m > \dfrac{3}{2}\end{array}\)

Vậy \(m > \dfrac{3}{2}\).

Phương pháp giải:

- Sử dụng công thức tính đạo hàm hàm hợp \(\left( {{u^n}} \right)' = n.{u^{n - 1}}.u'\).

- Sử dụng các công thức tính đạo hàm hàm lượng giác: \(\left( {\sin u} \right)' = u'.\cos u\), \(\left( {\cos u} \right)' =  - u'.\sin u\).

- Sử dụng công thức nhân đôi: \(2\sin x\cos x = \sin 2x\).

Lời giải chi tiết:

Ta có: \(y' = 1 + \dfrac{{2x}}{{2\sqrt {{x^2} + 1} }} = 1 + \dfrac{x}{{\sqrt {{x^2} + 1} }} = \dfrac{{\sqrt {{x^2} + 1}  + x}}{{\sqrt {{x^2} + 1} }}\).

\(\begin{array}{l} \Rightarrow \dfrac{{y'}}{y} = \dfrac{{\sqrt {{x^2} + 1}  + x}}{{\sqrt {{x^2} + 1} }}:\left( {x + \sqrt {{x^2} + 1} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{\sqrt {{x^2} + 1}  + x}}{{\sqrt {{x^2} + 1} }}.\dfrac{1}{{x + \sqrt {{x^2} + 1} }} = \dfrac{1}{{\sqrt {{x^2} + 1} }}\end{array}\)

Chọn A.

Phương pháp giải:

- Tính \(y'\), sử dụng công thức \(\left( {{x^n}} \right)' = n.{x^{n - 1}}\).

- Tam thức bậc hai \(a{x^2} + bx + c\,\,\left( {a \ne 0} \right) \ge 0\,\,\forall x \in \mathbb{R} \Leftrightarrow \left\{ \begin{array}{l}a > 0\\\Delta  \le 0\end{array} \right.\).

Lời giải chi tiết:

\(\begin{array}{l}y = \dfrac{1}{3}{x^3} - 2m{x^2} + \left( {m + 3} \right)x - 5 + m\\ \Rightarrow y' = {x^2} - 4mx + m + 3\\y' \ge 0\,\,\forall x \in \mathbb{R}\\ \Leftrightarrow \left\{ \begin{array}{l}a = 1 > 0\\\Delta ' = 4{m^2} - m - 3 \le 0\end{array} \right.\\ \Leftrightarrow  - \dfrac{3}{4} \le m \le 1\end{array}\)

Chọn C.

Phương pháp giải:

- Tính \(y'\).

- Phương trình bậc hai \(a{x^2} + bx + c = 0\,\,\left( {a \ne 0} \right)\) có 2 nghiệm trái dấu khi và chỉ khi \(ac < 0\).

Lời giải chi tiết:

Ta có: \(y' = f'\left( x \right) = 3m{x^2} + 2x + 1\).

Để \(f'\left( x \right) = 0\) có hai nghiệm trái dấu thì \(\left\{ \begin{array}{l}3m \ne 0\\3m.1 < 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m < 0\end{array} \right. \Leftrightarrow m < 0\).

Chọn C.

Phương pháp giải:

+) Tính đạo hàm của hàm số khi \(x > 1\)

+) Tính đạo hàm của hàm số khi \(x < 1\)

+) Sử dụng định nghĩa đạo hàm, xét sự tồn tại của đạo hàm của hàm số tại x = 1.

Lời giải chi tiết:

Với \(x > 1\) ta có: \(f\left( x \right) = {x^2} - 3x + 1 \Rightarrow f'\left( x \right) = 2x - 3\)

Với \(x < 1\) ta có : \(f\left( x \right) = 2x + 2 \Leftrightarrow f'\left( x \right) = 2\)

Với x = 1 ta có : \(\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{x^2} - 3x + 1} \right) =  - 1 \ne f\left( 1 \right) = 4 \Rightarrow \) Hàm số không liên tục tại x = 1, do đó không có đạo hàm tại x = 1.

Vậy \(f'\left( x \right) = \left\{ \matrix{  2x - 3\,\,\,khi\,\,x > 1 \hfill \cr   2\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x < 1 \hfill \cr}  \right.\)

Chọn B.

Phương pháp giải:

Tính đạo hàm của hàm số.

Giải bpt \(y' \le 0\,\,\forall x \in R\)

Lời giải chi tiết:

\(\eqalign{  & y = {{m{x^3}} \over 3} - m{x^2} + \left( {3m - 1} \right)x + 1  \cr   &  \Rightarrow y' = m{x^2} - 2mx + 3m - 1  \cr   & y' \le 0\,\,\forall x \in R \Rightarrow m{x^2} - 2mx + 3m - 1 \le 0\,\,\forall x \in R \cr} \)

TH1: m = 0, khi đó \(BPT \Leftrightarrow  - 1 \le 0\), đúng \(\forall x \in R\)

TH2: \(\eqalign{  & m \ne 0 \Leftrightarrow y' \le 0\,\,\forall x \in R \Leftrightarrow \left\{ \matrix{  a = m < 0 \hfill \cr   \Delta ' = {m^2} - m\left( {3m - 1} \right) \le 0 \hfill \cr}  \right.  \cr   &  \Leftrightarrow \left\{ \matrix{  m < 0 \hfill \cr    - 2{m^2} + m \le 0 \hfill \cr}  \right. \Leftrightarrow \left\{ \matrix{  m < 0 \hfill \cr   \left[ \matrix{  m \le 0 \hfill \cr   m \ge {1 \over 2} \hfill \cr}  \right. \hfill \cr}  \right. \Leftrightarrow m < 0 \cr} \)

Kết hợp cả 2 trường hợp ta có \(m \le 0\) là những giá trị cần tìm.

Chọn C.

Phương pháp giải:

Tính y’, giải bất phương trình.

Lời giải chi tiết:

Ta có: \(y' = \left( {{m^2} - 1} \right){x^2} + 2\left( {m - 1} \right)x - 2\)

\(\eqalign{  &  \Rightarrow y' - 2x - 2 > 0\,\,\forall x \in R  \cr   &  \Leftrightarrow \left( {{m^2} - 1} \right){x^2} + 2\left( {m - 1} \right)x - 2 - 2x - 2 > 0\,\,\,\forall x \in R  \cr   &  \Leftrightarrow \left( {{m^2} - 1} \right){x^2} + 2\left( {m - 2} \right)x - 4 > 0\,\,\,\forall x \in R \cr} \)

TH1: \({m^2} - 1 = 0 \Leftrightarrow m =  \pm 1\)

Khi m = 1 ta có: \( - 2x - 4 > 0\,\,\,\forall x \in R \Leftrightarrow x <  - 2\,\forall x \in R\,\,\left( {ktm} \right)\)

Khi \(m =  - 1\) ta có: \( - 6x - 4 > 0\,\,\forall x \in R \Leftrightarrow x < {{ - 2} \over 3}\,\,\forall x \in R\,\,\left( {ktm} \right)\)

TH2 :  \({m^2} - 1 \ne 0 \Leftrightarrow m \ne  \pm 1\)

Khi đó

\(\eqalign{
& \left( {{m^2} - 1} \right){x^2} + 2\left( {m - 2} \right)x - 4 > 0\,\,\,\forall x \in R \Leftrightarrow \left\{ \matrix{
{m^2} - 1 > 0 \hfill \cr
\Delta ' = {\left( {m - 2} \right)^2} + 4\left( {{m^2} - 1} \right) < 0 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
\left[ \matrix{
m > 1 \hfill \cr
m < - 1 \hfill \cr} \right. \hfill \cr
5{m^2} - 4m < 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
\left[ \matrix{
m > 1 \hfill \cr
m < - 1 \hfill \cr} \right. \hfill \cr
0 < m < {4 \over 5} \hfill \cr} \right. \Leftrightarrow m \in \emptyset \cr} \)

Vậy không có giá trị nào của m thỏa mãn yêu cầu bài toán.

Chọn C.

Phương pháp giải:

+) Do \(P\left( x \right)\) bậc 3 và có 3 nghiệm phân biệt \({x_1},{x_2},{x_3}\) nên \(P\left( x \right)\) được biểu diễn dưới dạng \(P\left( x \right) = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\,\,\left( {a \ne 0} \right)\).

+) Tính \(P'\left( x \right)\), từ đó tính \(P'\left( {{x_1}} \right);\,\,P'\left( {{x_2}} \right);\,\,P'\left( {{x_3}} \right)\).

+) Thay vào biểu thức \(\dfrac{1}{{P'\left( {{x_1}} \right)}} + \dfrac{1}{{P'\left( {{x_2}} \right)}} + \dfrac{1}{{P'\left( {{x_3}} \right)}}\). Quy đồng và rút gọn.

Lời giải chi tiết:

Do \(P\left( x \right)\) bậc 3 và có 3 nghiệm phân biệt \({x_1},{x_2},{x_3}\) nên \(P\left( x \right)\) được biểu diễn dưới dạng \(P\left( x \right) = a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)\,\,\left( {a \ne 0} \right)\).

Ta có: \(P'\left( x \right) = a\left( {x - {x_2}} \right)\left( {x - {x_3}} \right) + a\left( {x - {x_1}} \right)\left( {x - {x_3}} \right) + a\left( {x - {x_1}} \right)\left( {x - {x_2}} \right)\)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}P\left( {{x_1}} \right) = a\left( {{x_1} - {x_2}} \right)\left( {{x_1} - {x_3}} \right)\\P\left( {{x_2}} \right) = a\left( {{x_2} - {x_1}} \right)\left( {{x_2} - {x_3}} \right)\\P\left( {{x_3}} \right) = a\left( {{x_3} - {x_1}} \right)\left( {{x_3} - {x_2}} \right)\end{array} \right.\\ \Rightarrow \dfrac{1}{{P'\left( {{x_1}} \right)}} + \dfrac{1}{{P'\left( {{x_2}} \right)}} + \dfrac{1}{{P'\left( {{x_3}} \right)}}\\ = \dfrac{1}{{a\left( {{x_1} - {x_2}} \right)\left( {{x_1} - {x_3}} \right)}} + \dfrac{1}{{a\left( {{x_2} - {x_1}} \right)\left( {{x_2} - {x_3}} \right)}} + \dfrac{1}{{a\left( {{x_3} - {x_1}} \right)\left( {{x_3} - {x_2}} \right)}}\\ = \dfrac{{ - {x_2} + {x_3} - {x_3} + {x_1} - {x_1} + {x_2}}}{{a\left( {{x_1} - {x_2}} \right)\left( {{x_2} - {x_3}} \right)\left( {{x_3} - {x_1}} \right)}} = 0 \end{array}\)

Phương pháp giải:

Sử dụng hệ thức Vi-et cho phương trình bậc ba \(a{x^3} + b{x^2} + cx + d = 0\,\left( {a \ne 0} \right)\) có ba nghiệm \({x_1},{x_2},{x_3}\)

\(\left\{ \begin{array}{l}{x_1} + {x_2} + {x_3} = \dfrac{{ - b}}{a}\\{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} = \dfrac{c}{a}\\{x_1}{x_2}{x_3} =  - \dfrac{d}{a}\end{array} \right.\)

Sau đó biến đổi \(f'\left( x \right)\) để tính \(P.\)

Lời giải chi tiết:

Ta có \(f\left( x \right) = {2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018\)

\( \Rightarrow f'\left( x \right) = {3.2^{2019}}{x^2} + {3.2^{2019}}x = {3.2^{2019}}x\left( {x + 1} \right)\) \( \Rightarrow \dfrac{1}{{f'\left( x \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}.\dfrac{1}{{x.\left( {x + 1} \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}\left( {\dfrac{1}{x} - \dfrac{1}{{x + 1}}} \right)\)

Xét phương trình hoành độ giao điểm của đồ thị hàm số với trục hoành \({2^{2019}}{x^3} + {3.2^{2018}}{x^2} - 2018 = 0\) (*)

Vì \({x_1},{x_2},{x_3}\) là ba ngiệm của phương trình (*) nên theo hẹ thức Vi-et ta có

\(\left\{ \begin{array}{l}{x_1} + {x_2} + {x_3} = \dfrac{{ - 3}}{2}\\{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} = 0\\{x_1}{x_2}{x_3} = \dfrac{{2018}}{{{2^{2019}}}}\end{array} \right.\)

Ta có \(P = \dfrac{1}{{f'\left( {{x_1}} \right)}} + \dfrac{1}{{f'\left( {{x_2}} \right)}} + \dfrac{1}{{f'\left( {{x_3}} \right)}} = \dfrac{1}{{{{3.2}^{2019}}}}\left( {\dfrac{1}{{{x_1}}} - \dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2}}} - \dfrac{1}{{{x_2} + 1}} + \dfrac{1}{{{x_3}}} - \dfrac{1}{{{x_3} + 1}}} \right)\)

\( = \dfrac{1}{{{{3.2}^{2019}}}}\left[ {\left( {\dfrac{1}{{{x_1}}} + \dfrac{1}{{{x_2}}} + \dfrac{1}{{{x_3}}}} \right) - \left( {\dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2} + 1}} + \dfrac{1}{{{x_3} + 1}}} \right)} \right]\)

\( = \dfrac{1}{{{{3.2}^{2019}}}}\left[ {\dfrac{{{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3}}}{{{x_1}{x_2}{x_3}}} - \dfrac{{\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right) + \left( {{x_1} + 1} \right)\left( {{x_3} + 1} \right) + \left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}}} \right]\)

\( = \dfrac{1}{{{{3.2}^{2019}}}}\left( {0 - \dfrac{{{x_1}{x_2} + {x_2}{x_3} + {x_1}{x_3} + 2\left( {{x_1} + {x_2} + {x_3}} \right) + 3}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}}} \right)\)

\( = \dfrac{1}{{{{3.2}^{2019}}}}.\dfrac{{0 + 2.\dfrac{{ - 3}}{2} + 3}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)\left( {{x_3} + 1} \right)}} = 0\)

Chọn C.

Phương pháp giải:

Tính đạo hàm của hàm số.

Giải bpt \(y' \le 0\,\,\forall x \in R\)

Lời giải chi tiết:

\(\begin{array}{l}y = \frac{{m{x^3}}}{3} - m{x^2} + \left( {3m - 1} \right)x + 1\\ \Rightarrow y' = m{x^2} - 2mx + 3m - 1\\y' \le 0\,\,\forall x \in R \Rightarrow m{x^2} - 2mx + 3m - 1 \le 0\,\,\forall x \in R\end{array}\)

TH1: m = 0, khi đó \(BPT \Leftrightarrow  - 1 \le 0\) , đúng \(\forall x \in R\)

TH2: \(\begin{array}{l}m \ne 0 \Leftrightarrow y' \le 0\,\,\forall x \in R \Leftrightarrow \left\{ \begin{array}{l}a = m < 0\\\Delta ' = {m^2} - m\left( {3m - 1} \right) \le 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m < 0\\ - 2{m^2} + m \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m < 0\\\left[ \begin{array}{l}m \le 0\\m \ge \frac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow m < 0\end{array}\)

Kết hợp cả 2 trường hợp ta có \(m \le 0\) là những giá trị cần tìm.

Chọn C.